题目内容
如果函数y=x4-8x2+c在[-1,3]上的最小值是-14,求y的最大值.
考点:函数的最值及其几何意义
专题:导数的综合应用
分析:求函数的导数,结合函数的最小值为-14,求出c的值即可得到结论.
解答:
解:由y′=4x3-16x=4x(x2-4)=0,
解得x=0,-2,2,
分别求出f(-2)=c-16,f(2)=c-16,
则最小值为c-16=-14,c=2,
则函数f(x)=x4-8x2+2,
则f(0)=2,f(-1)=(-1)4-8(-1)2+2=1-8+2=-5,
f(3)=34-8×32+2=11,
故函数的最大值为11.
解得x=0,-2,2,
分别求出f(-2)=c-16,f(2)=c-16,
| x | -1 | (-1,0) | 0 | (0,2) | 2 | (2,3) | 3 |
| y′ | + | 0 | - | 0 | + | ||
| y | ↗ | 极大 | ↘ | 极小 | ↗ |
则函数f(x)=x4-8x2+2,
则f(0)=2,f(-1)=(-1)4-8(-1)2+2=1-8+2=-5,
f(3)=34-8×32+2=11,
故函数的最大值为11.
点评:本题考查了利用导数求闭区间上函数的最值,求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
对任意x,y∈R,函数f(x)都满足f(x+y)=f(x)+f(y)+2恒成立,则f(5)+f(-5)等于( )
| A、0 | B、-4 | C、-2 | D、2 |
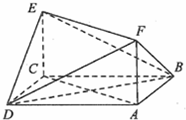 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=