题目内容
1.方程x2+(4+i)x+4+ai=0(a∈R)有实根b,且z=a+bi,则z=( )| A. | 2-2i | B. | 2+2i | C. | -2+2i | D. | -2-2i |
分析 由复数相等的意义将方程x2+(4+i)x+4+ai=0(a∈R)转化为实系数方程,解方程求出两根.
解答 解:方程x2+(4+i)x+4+ai=0(a∈R)可以变为x2+4x+4+i(x+a)=0,
由复数相等的意义得 $\left\{\begin{array}{l}{{x}^{2}+4x+4=0}\\{x+a=0}\end{array}\right.$,解得x=-2,a=2,
方程x2+(4+i)x+4+ai=0(a∈R)有实根b,故b=-2,
所以复数z=2-2i,
故选:A.
点评 本题考查复数相等的意义,两个复数相等,则它们的实部与实部相等,虚部与虚部相等.

练习册系列答案
相关题目
12.某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图1)和女生身高情况的频率分布直方图(图2).已知图1中身高在170~175cm的男生人数有16人.
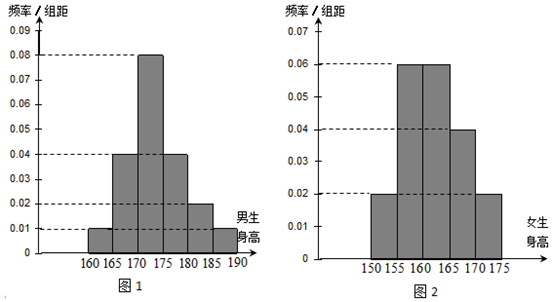
(1)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
(2)在上述80名学生中,从身高在170-175cm之间的学生按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式及参考数据如下:${k^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$

(1)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
参考公式及参考数据如下:${k^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.025 | 0.610 | 0.005 | 0.001 |
| k0 | 5.024 | 4.635 | 7.879 | 10.828 |
10.设等差数列{an}的前n项和为Sn,且S2015>0,S2016<0.则数列{$\frac{{S}_{n}}{{a}_{n}}$}的最大的项的n的值为( )
| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |