题目内容
设函数f（x）=-a+
，g（x）=ax+a，若恒有f（x）≤g（a）成立，试求实数a的取值范围．
| -x2+4x |
考点：函数恒成立问题
专题：函数的性质及应用
分析：先求函数f（x）的定义域，确定x的范围，化简f（x）≤g（a）为a≥
，令t=x+2，构造函数h（t）=
，化简后得h（t）=
，根据t的范围求h（x）的最大值，即可求出实数a的取值范围．
| ||
| x+2 |
| ||
| t |
-12(
|
解答：
解：∵f（x）=-a+
，
∴-x2+4x≥0
解得0≤x≤4，
∵f（x）=-a+
，g（x）=ax+a，
∴f（x）≤g（a）可化为
-a+
≤ax+a，
即
≤（x+2）a
∵x+2＞0
∴a≥
，…①
令t=x+2，则2≤t≤6，
①式可化为，a≥
，
即a≥
，
令h（t）=
=
=
，
∵2≤t≤6，
∴
≤
≤
，
∴h（t）在t=3时，取最大值，且h(3)=
，
∴a≥
．
∴实数a的取值范围是[
，+∞)．
| -x2+4x |
∴-x2+4x≥0
解得0≤x≤4，
∵f（x）=-a+
| -x2+4x |
∴f（x）≤g（a）可化为
-a+
| -x2+4x |
即
| -x2+4x |
∵x+2＞0
∴a≥
| ||
| x+2 |
令t=x+2，则2≤t≤6，
①式可化为，a≥
| ||
| t |
即a≥
| ||
| t |
令h（t）=
| ||
| t |
-
|
=
-12(
|
∵2≤t≤6，
∴
| 1 |
| 6 |
| 1 |
| t |
| 1 |
| 2 |
∴h（t）在t=3时，取最大值，且h(3)=
| ||
| 3 |
∴a≥
| ||
| 3 |
∴实数a的取值范围是[
| ||
| 3 |
点评：本题考查函数定义域，不等式的化简，配方法求函数最大值的技巧，以及恒成立问题的转化等综合知识，属于难题．
练习册系列答案
名校课堂系列答案
相关题目
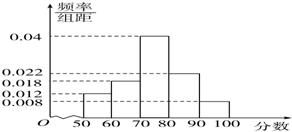某市的教育研究机构对全市高三学生进行综合素质测试，随机抽取了部分学生的成绩，得到如图所示的成绩频率分布直方图．