题目内容

设口袋中有黑球、白球共7 个，从中任取2个球，已知取到至少1个白球的概率为
5
7
，则口袋中白球的个数为
 
．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：设口袋中白球个数为x个，由对立事件概率公式得到1-
C
2
7-x
C
2
7
=
5
7
，由此能求出口袋中白球的个数．
解答： 解：设口袋中白球个数为x个，
由已知得1-
C
2
7-x
C
2
7
=
5
7
，
解得x=3．
故答案为：3．
点评：本题考查口袋中白球的个数的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．
练习册系列答案
相关题目
已知
a
=（1，1），
b
=（-2，-3），
c
=（2，0），且
c
=m
a
+n
b
，求m，n的值．
已知函数y=1-2cos2x+5sinx，求函数的值域．
设m是正整数，试证下列等式
（1）
∫
π
-π
sinmxdx=0   
（2）
∫
π
-π
cosmxdx=0  
（3）
∫
π
-π
sin2mxdx=π 
（4）
∫
π
-π
cos2mxdx=π
若函数f（x）=sin（ωx-
π
4
）（ω＞0）在区间（0，
π
2
）上单调递增，则ω的取值范围是（　　）
A、（0，
3
2
]
B、[1，
3
2
]
C、[1，2]
D、（0，2]
设f（x）=msin（πx+α1）+ncos（πx+α2），其中m、n、α1、α2都是非零实数，若f（2004）=1，则f（2005）=
 
．
设函数 f（ x）的定义域为D，D⊆[0，4π]，它的对应法则为 f：x→sin x，现已知 f（ x）的值域为{0，-
1
2
，1}，则这样的函数共有
 
个．
已知角θ的始边与x轴的非负半轴重合，终边过点P（-3，4），则sin（θ+
π
4
）=
 
．
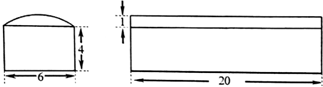
某校新校区建设在市二环路主干道旁，因安全需要，挖掘建设了一条人行地下通道，地下通道设计三视图中的主（正）视力（其中上部分曲线近似为抛物）和侧（左）视图如图（单位：m），则该工程需挖掘的总土方数为（　　）
A、560m3
B、540m3
C、520m3
D、500m3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网