题目内容
设函数 f( x)的定义域为D,D⊆[0,4π],它的对应法则为 f:x→sin x,现已知 f( x)的值域为{0,-
,1},则这样的函数共有 个.
| 1 |
| 2 |
考点:映射
专题:函数的性质及应用,集合
分析:分别求出sinx=0,x=0,π,2π,3π,4π,
sinx=-
,x=
,x=
,x=
,x=
,
sinx=1,x=
,x=
利用排列组合知识求解得出这样的函数共有:(C
+C
)(
)(
)即可.
sinx=-
| 1 |
| 2 |
| 7π |
| 6 |
| 11π |
| 6 |
| 19π |
| 6 |
| 23π |
| 6 |
sinx=1,x=
| π |
| 2 |
| 5π |
| 2 |
利用排列组合知识求解得出这样的函数共有:(C
1 5 |
2 5 |
| +C | 3 5 |
| +C | 4 5 |
| +C | 5 5 |
| C | 1 4 |
| +C | 2 4 |
| +C | 3 4 |
| +C | 4 4 |
| C | 1 2 |
| +C | 2 2 |
解答:
解:∵函数 f( x)的定义域为D,D⊆[0,4π],
∴它的对应法则为 f:x→sin x,
f( x)的值域为{0,-
,1},
sinx=0,x=0,π,2π,3π,4π,
sinx=-
,x=
,x=
,x=
,x=
,
sinx=1,x=
,x=
这样的函数共有:(C
+C
)(
)(
)=31×15×3=1395
故答案为:1395
∴它的对应法则为 f:x→sin x,
f( x)的值域为{0,-
| 1 |
| 2 |
sinx=0,x=0,π,2π,3π,4π,
sinx=-
| 1 |
| 2 |
| 7π |
| 6 |
| 11π |
| 6 |
| 19π |
| 6 |
| 23π |
| 6 |
sinx=1,x=
| π |
| 2 |
| 5π |
| 2 |
这样的函数共有:(C
1 5 |
2 5 |
| +C | 3 5 |
| +C | 4 5 |
| +C | 5 5 |
| C | 1 4 |
| +C | 2 4 |
| +C | 3 4 |
| +C | 4 4 |
| C | 1 2 |
| +C | 2 2 |
故答案为:1395
点评:本题考查了映射,函数的概念,排列组合的知识,难度不大,但是综合性较强.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
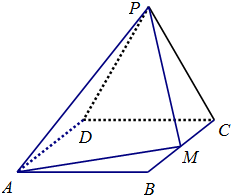 如图,已知边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2
如图,已知边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2