题目内容
在正方体ABCD-A1B1C1D1中,直线AD1与平面BB1D1D所成角的余弦值是 .
考点:直线与平面所成的角
专题:计算题,空间角
分析:在正方体ABCD-A1B1C1D1中,证明HA⊥平面BD1,则根据线面角的定义∠AD1H就是直线AD1平面BD1所成角,解直角三角形AD1H即可.
解答:
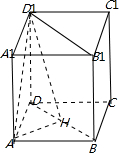 解:取BD的中点H连接AH,∵正方体ABCD-A1B1C1D1
解:取BD的中点H连接AH,∵正方体ABCD-A1B1C1D1
∴BB1⊥平面AC,
∴AH⊥BB1,
又∴AH⊥BD且BD∩BB1=B,
∴AH⊥面BD1,
∴AH⊥D1H,
∴∠AD1H就是直线AD1与平面BD1所成角,
在直角三角形AHD1中设AB=1则AH=
,AD1=
∴sin∠AD1H=
=
∴cos∠AD1H=
.
故答案为:
.
 解:取BD的中点H连接AH,∵正方体ABCD-A1B1C1D1
解:取BD的中点H连接AH,∵正方体ABCD-A1B1C1D1∴BB1⊥平面AC,
∴AH⊥BB1,
又∴AH⊥BD且BD∩BB1=B,
∴AH⊥面BD1,
∴AH⊥D1H,
∴∠AD1H就是直线AD1与平面BD1所成角,
在直角三角形AHD1中设AB=1则AH=
| ||
| 2 |
| 2 |
∴sin∠AD1H=
| AH |
| AD1 |
| 1 |
| 2 |
∴cos∠AD1H=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查直线和平面所成的角,求直线和平面所成的角关键是找到斜线在平面内的射影,把空间角转化为平面角求解,属基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
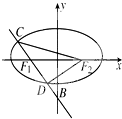 已知椭圆
已知椭圆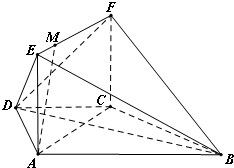 如图,在梯形ABCD中,AD⊥CD,AB∥CD,AD=CD=
如图,在梯形ABCD中,AD⊥CD,AB∥CD,AD=CD=