题目内容
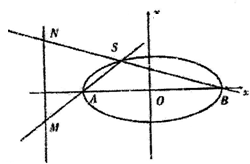 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| ||
| 2 |
| 10 |
| 3 |
(1)求椭圆C的方程;
(2)若A为线段MS的中点,求△SAB的面积;
(3)求线段MN长度的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
=
,c2=
a2=a2-1,由此能求出椭圆C的方程.
(2)由(1)知A(-2,0),B(2,0),设S(x0,y0),则x0=-4+
=-
,y0=
=
=
,由此能求出△SAB的面积.
(3)设直线AS的斜率为k(k>0),则lAS:y=k(x+2),M(-
,-
k),由
,得(1+4k2)x2+16k2x+16k2-4=0,由此利用韦达定理和均值定理能求出|MN|的最小值.
| c |
| a |
| ||
| 2 |
| 3 |
| 4 |
(2)由(1)知A(-2,0),B(2,0),设S(x0,y0),则x0=-4+
| 10 |
| 3 |
| 2 |
| 3 |
1-
|
1-
|
2
| ||
| 3 |
(3)设直线AS的斜率为k(k>0),则lAS:y=k(x+2),M(-
| 10 |
| 3 |
| 4 |
| 3 |
|
解答:
(本小题满分14分)
解:(1)∵椭圆C:
+y2=1(a>1)的离心率为
,
∴
=
,…(1分)
∴c2=
a2=a2-1,…(2分)
∴a2=4,
∴椭圆C的方程为
+y2=1.…(3分)
(2)由(1)知A(-2,0),B(2,0),
设S(x0,y0),∵A为线段MS的中点,
∴-2=
,…(4分)
∴x0=-4+
=-
,
∴y0=
=
=
,…(5分)
∴△SAB的面积为:
|AB|•y0=
×4×
=
.…(7分)
(3)设直线AS的斜率为k(k>0),
则lAS:y=k(x+2),M(-
,-
k)…(8分)
由
,消得y得x2+4[k(x+2)]2=4,
即(1+4k2)x2+16k2x+16k2-4=0,…(9分)
∴xA•xS=(-2)•xS=
,
∴xS=
,…(10分)
将xS代入y=k(x+2),得yS=
,即S(
,
),
∴kBS=
=-
,
∴直线BS的方程为:y=-
(x-2),…(11分)
∴yN=-
(-
-2)=
,
∴|MN|=|yN-yM|=|
-(-
k)|…(12分)
=
|
+k|=
(
+k)≥
,…(13分)
当且仅当
=k即k=1时等号成立,
∴|MN|的最小值为
.…(14分)
解:(1)∵椭圆C:
| x2 |
| a2 |
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
∴c2=
| 3 |
| 4 |
∴a2=4,
∴椭圆C的方程为
| x2 |
| 4 |
(2)由(1)知A(-2,0),B(2,0),
设S(x0,y0),∵A为线段MS的中点,
∴-2=
-
| ||
| 2 |
∴x0=-4+
| 10 |
| 3 |
| 2 |
| 3 |
∴y0=
1-
|
1-
|
2
| ||
| 3 |
∴△SAB的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
4
| ||
| 3 |
(3)设直线AS的斜率为k(k>0),
则lAS:y=k(x+2),M(-
| 10 |
| 3 |
| 4 |
| 3 |
由
|
即(1+4k2)x2+16k2x+16k2-4=0,…(9分)
∴xA•xS=(-2)•xS=
| 16k2-4 |
| 1+4k2 |
∴xS=
| 2-8k2 |
| 1+4k2 |
将xS代入y=k(x+2),得yS=
| 4k |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
∴kBS=
| ||
|
| 1 |
| 4k |
∴直线BS的方程为:y=-
| 1 |
| 4k |
∴yN=-
| 1 |
| 4k |
| 10 |
| 3 |
| 4 |
| 3k |
∴|MN|=|yN-yM|=|
| 4 |
| 3k |
| 4 |
| 3 |
=
| 4 |
| 3 |
| 1 |
| k |
| 4 |
| 3 |
| 1 |
| k |
| 8 |
| 3 |
当且仅当
| 1 |
| k |
∴|MN|的最小值为
| 8 |
| 3 |
点评:本题考查椭圆方程的求法,考查三角形面积的求法,考查线段的最小值的求法,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设变量x,y满足
,若目标函数z=x-y+1的最小值为0,则m的值为( )
|
| A、4 | B、5 | C、6 | D、7 |
一个空间几何体的三视图如图所示,则该几何体的体积为( )
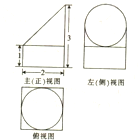

A、4+
| ||
| B、4+π | ||
| C、4+2π | ||
| D、以上都不对 |
在实数范围内,不等式||x-2|-1|≤1的解集为( )
| A、(0,4] |
| B、[0,4) |
| C、[0,4] |
| D、[1,4] |
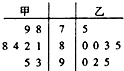 甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示.
甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示. 如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=