题目内容
2．己知i是虚数单位，$\overline z$是z的共轭复数，$（{2-i}）\overline z=3-4i$，则z的虚部为（ ）| A． | 1 | B． | -1 | C． | i | D． | -i |
分析 把已知等式变形，利用复数代数形式的乘除运算化简求得$\overline{z}$，进一步得到z得答案．
解答 解：由$（{2-i}）\overline z=3-4i$，得
$\overline{z}=\frac{3-4i}{2-i}=\frac{（3-4i）（2+i）}{（2-i）（2+i）}=\frac{10-5i}{5}=2-i$，
∴z=2+i．
则z的虚部为1．
故选：A．
点评 本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
12．在复平面内，复数$\frac{2}{1+i}$（i为虚数单位）对应的点与原点的距离是（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | $2\sqrt{2}$ |
已知△ABC中，顶点A（7，-3），AC边上的高BH所在直线方程为x-2y-5=0，AB边上的中线CM所在的直线方程为6x-y-21=0．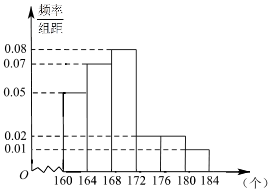
《汉字听写大会》不断创收视新高，为了避免“书写危机”弘扬传统文化，某市对全市10万名市民进行了汉字听写测试，调查数据显示市民的成绩服从正态分布N（168，16）．现从某社区居民中随机抽取50名市民进行听写测试，发现被测试市民正确书写汉字的个数全部在160到184之间，将测试结果按如下方式分成六组：第一组[160，164），第二组[164，168），…，第六组[180，184），如图是按上述分组方法得到的频率分布直方图．