题目内容
已知向量
=
=(cosα,sinα),
=
=(2cosβ,2sinβ),
=
=(0,d)(d>0),其中O为坐标原点,且0<α<
<β<π.
(1)若
⊥(
-
),求β-α
(2)若
=1,
=
,求△OAB的面积S.
| OA |
| a |
| OB |
| b |
| OC |
| c |
| π |
| 2 |
(1)若
| a |
| b |
| a |
(2)若
| ||||
|
|
| ||||
|
|
| ||
| 2 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)两个向量垂直的充要条件是这两个向量的数量积为0,将
和(
-
)用坐标表示,求其数量积,再倒用两交差的余弦公式即可.
(2)由题意可得
•
=
,即1×2×cos∠AOB=
,求得cos∠AOB的值,可得sin∠AOB的值,从而求得△OAB的面积S=
|
|•|
|•sin∠AOB 的值.
| a |
| b |
| a |
(2)由题意可得
| OA |
| OB |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| OA |
| OB |
解答:
解:(1)∵
⊥(
-
),∴
•(
-
)=
•
-
2=2cosαcosβ+2sinαsinβ-1=2cos(α-β)-1=0,
即cos(α-β)=
,即cos(β-α)=
.
再结合0<α<
<β<π,∴0<β-α<π,可得β-α=
.
(2)由题意可得,|
|=1,|
|=2,
∵
=1,
=
,相乘可得
•
=
,即1×2×cos∠AOB=
,
∴cos∠AOB=
,
∴sin∠AOB=
,
∴△OAB的面积S=
|
|•|
|•sin∠AOB=
×1×2×
=
.
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
| a |
即cos(α-β)=
| 1 |
| 2 |
| 1 |
| 2 |
再结合0<α<
| π |
| 2 |
| π |
| 3 |
(2)由题意可得,|
| OA |
| OB |
∵
| ||||
|
|
| ||||
|
|
| ||
| 2 |
| OA |
| OB |
| ||
| 2 |
| ||
| 2 |
∴cos∠AOB=
| ||
| 4 |
∴sin∠AOB=
| ||
| 4 |
∴△OAB的面积S=
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
点评:本题综合考查了向量数量积的运算性质和三角变换公式的应用,解题时要耐心细致,认真观察,属于基础题.

练习册系列答案
相关题目
若二面角α-L-β的大小为
,此二面角的张口内有一点P到α、β的距离分别为1和2,则P点到棱l的距离是( )
| π |
| 3 |
A、
| ||||
| B、2 | ||||
C、2
| ||||
D、2
|
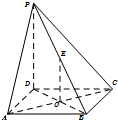 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,AC与BD交于点O,E为PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,AC与BD交于点O,E为PB的中点.