题目内容
设{an}是递增等差数列,其前n项和为Sn,已知a1=1,且S2,a4+1,S4成等比数列,数列{bn}满足an=2log3bn-1(n∈N+).
(1)求数列{an},{bn}的通项公式;
(2)令Cn=
(n∈N+),求数列{cn}的前n项和Tn.
(1)求数列{an},{bn}的通项公式;
(2)令Cn=
| an |
| bn |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)设等差数列{an}的公差d>0,由于S2,a4+1,S4成等比数列,可得(a4+1)2=S2S4,利用等差数列的通项公式与前n项和公式即可得出.
(2)利用“错位相减法”与等比数列的前n项和公式即可得出.
(2)利用“错位相减法”与等比数列的前n项和公式即可得出.
解答:
解:(1)设等差数列{an}的公差d>0,
∵S2,a4+1,S4成等比数列,
∴(a4+1)2=S2S4,
∴(a1+3d+1)2=(2a1+d)(4a1+
d),
即(2+3d)2=(2+d)(4+6d),
解得d=2.
∴an=1+2(n-1)=2n-1.
∵an=2log3bn-1(n∈N+).
∴2n-1=2log3bn-1.
∴bn=3n.
(2)cn=
=
.
∴Tn=
+
+
+…+
+
,
Tn=
+
+
+…+
+
,
∴
Tn=
+
+
+…+
-
=
-
-
=
-
,
∴Tn=1-
.
∵S2,a4+1,S4成等比数列,
∴(a4+1)2=S2S4,
∴(a1+3d+1)2=(2a1+d)(4a1+
| 4×3 |
| 2 |
即(2+3d)2=(2+d)(4+6d),
解得d=2.
∴an=1+2(n-1)=2n-1.
∵an=2log3bn-1(n∈N+).
∴2n-1=2log3bn-1.
∴bn=3n.
(2)cn=
| an |
| bn |
| 2n-1 |
| 3n |
∴Tn=
| 1 |
| 3 |
| 3 |
| 32 |
| 5 |
| 33 |
| 2n-3 |
| 3n-1 |
| 2n-1 |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 3 |
| 33 |
| 5 |
| 34 |
| 2n-3 |
| 3n |
| 2n-1 |
| 3n+1 |
∴
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 32 |
| 2 |
| 33 |
| 2 |
| 3n |
| 2n-1 |
| 3n+1 |
| ||||
1-
|
| 1 |
| 3 |
| 2n-1 |
| 3n+1 |
| 2 |
| 3 |
| 2n+2 |
| 3n+1 |
∴Tn=1-
| n+1 |
| 3n |
点评:本题考查了等差数列与等比数列的通项公式与前n项和公式、对数的运算性质、“错位相减法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x-1)是定义在R上的奇函数,若对于任意两个实数x1≠x2,不等式
>0恒成立,则不等式f(x+3)<0的解集为( )
| f(x1)-f(x2) |
| x1-x2 |
| A、(-∞,-3) |
| B、(4,+∞) |
| C、(-∞,1) |
| D、(-∞,-4) |
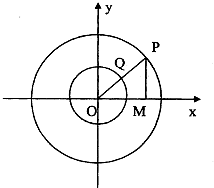 以原点为圆心的两个同心圆的方程分别为x2+y2=4和x2+y2=1,过原点O的射线交大圆于点P,交小圆于点Q,作PM⊥x轴于M,若
以原点为圆心的两个同心圆的方程分别为x2+y2=4和x2+y2=1,过原点O的射线交大圆于点P,交小圆于点Q,作PM⊥x轴于M,若 如图,焦点在x轴的椭圆C:
如图,焦点在x轴的椭圆C: