题目内容
在直角坐标系xoy中,动点P与定点F(1,0)的距离和它到定直线x=2的距离之比是
.
(Ⅰ)求动点P的轨迹Γ的方程;
(Ⅱ)设曲线Γ上的三点A(x1,y1),B(1,
),C(x2,y2)与点F的距离成等差数列,线段AC的垂直平分线与x轴的交点为T,求直线BT的斜率k.
| ||
| 2 |
(Ⅰ)求动点P的轨迹Γ的方程;
(Ⅱ)设曲线Γ上的三点A(x1,y1),B(1,
| ||
| 2 |
考点:轨迹方程,等差数列的通项公式
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由已知,得
=
,由此能求出动点P的轨迹C1的方程和轨迹是什么图形.
(Ⅱ)由已知可得|AF|=
(2-x1),|BF|=
(2-1),|CF|=
(2-x2)因为2|BF|=|AF|+|CF|,所以x1+x2=2,故线段AC的中点为(1,
),其垂直平分线方程为y-
=-
(x-1),由此能求出直线BT的斜率.
| ||
| |x-2| |
| ||
| 2 |
(Ⅱ)由已知可得|AF|=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| y1+y2 |
| 2 |
| y1+y2 |
| 2 |
| x1-x2 |
| y1-y2 |
解答:
解:(Ⅰ)由已知,得
=
.…(2分)
两边平方,化简得
+y2=1.
故轨迹Γ的方程是
+y2=1. …(4分)
(Ⅱ)由已知可得|AF|=
(2-x1),|BF|=
(2-1),|CF|=
(2-x2).…(6分)
因为2|BF|=|AF|+|CF|,所以
(2-x1)+
(2-x2)=2×
(2-1),
即得x1+x2=2,①…(5分).
故线段AC的中点为(1,
),
其垂直平分线方程为y-
=-
(x-1),②…(6分).
因为A,C在椭圆上,所以代入椭圆,两式相减,把①代入化简得:-
=y1+y2. ④…(10分)
把④代入②,令y=0得,x=0.5,∴点T的坐标为(0.5,0).…(11分)
∴直线BT的斜率k=
=
.…(12分)
| ||
| |x-2| |
| ||
| 2 |
两边平方,化简得
| x2 |
| 2 |
故轨迹Γ的方程是
| x2 |
| 2 |
(Ⅱ)由已知可得|AF|=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
因为2|BF|=|AF|+|CF|,所以
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
即得x1+x2=2,①…(5分).
故线段AC的中点为(1,
| y1+y2 |
| 2 |
其垂直平分线方程为y-
| y1+y2 |
| 2 |
| x1-x2 |
| y1-y2 |
因为A,C在椭圆上,所以代入椭圆,两式相减,把①代入化简得:-
| x1-x2 |
| y1-y2 |
把④代入②,令y=0得,x=0.5,∴点T的坐标为(0.5,0).…(11分)
∴直线BT的斜率k=
| ||||
| 1-0.5 |
| 2 |
点评:本题考查直线与圆锥曲线的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知全集U=R,集合M={x|x≥1},N={x|
≥1},则∁U(M∩N)=( )
| 3 |
| x-2 |
| A、{x|x<2} |
| B、{x|x≤2} |
| C、{x|-1<x≤2} |
| D、{x|-1≤x<2} |
已知数列{an}是等比数列,若a2a3a4=64,
=16,则(
)-2×2-3-(a5)
=( )
| a6a8 |
| 1 |
| 4 |
| 1 |
| 3 |
| A、4 | ||
| B、0 | ||
| C、0或-4 | ||
D、-
|
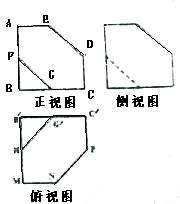 用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )
用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )| A、5 | ||
B、7-6
| ||
C、8-6
| ||
| D、4 |
“m>4”是“椭圆
+
=1(m>2)的焦距大于2”的( )
| x2 |
| m |
| y2 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,圆O为等腰梯形ABCD的外接圆,且AB∥CD,过点C作圆的切线CE交AB的延长线于E,证明:
如图,圆O为等腰梯形ABCD的外接圆,且AB∥CD,过点C作圆的切线CE交AB的延长线于E,证明: