Question

 已知抛物线，过定点的直线交抛物线于A、B两点.

(Ⅰ)分别过A、B作抛物线的两条切线，A、B为切点，求证：这两条切线的交点在定直线上.

(Ⅱ)当时，在抛物线上存在不同的两点P、Q关于直线对称，弦长|PQ|中是否存在最大值？若存在，求其最大值（用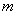表示），若不存在，请说明理由.

Answer 1

 解：(Ⅰ)由，得，设

过点A的切线方程为：，即

同理求得过点B的切线方程为：

∵直线PA、PB过，∴,

∴点在直线上，

∵直线AB过定点，∴，即

∴两条切线PA、PB的交点在定直线上.

(Ⅱ) 设，设直线的方程为：，则直线的方程为：，

，

，              ①

设弦PQ的中点，则

∵弦PQ的中点在直线上，

∴，即      ②

②代入①中，得            ③

由已知，当时， 弦长|PQ|中不存在最大值.

当时，这时，此时，弦长|PQ|中存在最大值，

即当时，弦长|PQ|中的最大值为