题目内容
定义在R上的奇函数f(x)满足:x≤0时,f(x)=ax+b(a>0且a≠1),f(1)=
,则f(2)=( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
| C、3 | ||
| D、-3 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据奇函数f(x)得f(0)=0,f(-1)=-
建立方程组,解之可求出a与b的值,从而求出x≤0时f(x)的解析式,再根据奇函数性质可求出所求.
| 1 |
| 2 |
解答:
解:∵定义在R上的奇函数f(x)
∴f(0)=f(-0)=-f(0)即f(0)=0
∵f(1)=
,∴f(-1)=-
∵x≤0时f(x)=ax+b
∴
,即
.
即f(x)=2x-1(x≤0).
∴f(2)=-f(-2)=-(2-2-1)=
.
故选:B.
∴f(0)=f(-0)=-f(0)即f(0)=0
∵f(1)=
| 1 |
| 2 |
| 1 |
| 2 |
∵x≤0时f(x)=ax+b
∴
|
|
即f(x)=2x-1(x≤0).
∴f(2)=-f(-2)=-(2-2-1)=
| 3 |
| 4 |
故选:B.
点评:本题主要考查了函数奇偶性的性质,以及函数求值,同时考查了计算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=
+
(0<x<
)的最小值为( )
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
| A、169 | B、121 |
| C、25 | D、16 |
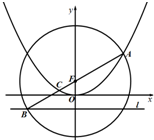 如图,已知点F是抛物线x2=4y的焦点,直线l为准线,点A是抛物线上一点.以F点为圆心,|AF|为半径作圆M交抛物线的准线l于点B.若A,B,F三点共线,则|AC|=( )
如图,已知点F是抛物线x2=4y的焦点,直线l为准线,点A是抛物线上一点.以F点为圆心,|AF|为半径作圆M交抛物线的准线l于点B.若A,B,F三点共线,则|AC|=( )A、
| ||
| B、16 | ||
C、
| ||
| D、8 |
在等差数列{an}中,已知a5+a7=16,则该数列前11项和S11的值是( )
| A、88 | B、58 |
| C、143 | D、176 |

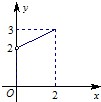 已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.
已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.