题目内容
已知四棱锥P-ABCD的顶点都在球O的球面上,底面ABCD是矩形,平面PAD⊥底面ABCD,△PAD为正三角形,AB=2AD=4,则球O的表面积为 .
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:求出△PAD所在圆的半径,利用勾股定理求出球O的半径R,即可求出球O的表面积.
解答:
解:令△PAD所在圆的圆心为O1,则圆O1的半径r=
,
因为平面PAD⊥底面ABCD,
所以OO1=
AB=2,
所以球O的半径R=
=
,
所以球O的表面积=4πR2=
.
故答案为:
.
2
| ||
| 3 |
因为平面PAD⊥底面ABCD,
所以OO1=
| 1 |
| 2 |
所以球O的半径R=
4+(
|
| 4 | ||
|
所以球O的表面积=4πR2=
| 64π |
| 3 |
故答案为:
| 64π |
| 3 |
点评:本题考查球O的表面积,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
当x、y满足不等式组
时,-2≤kx-y≤2恒成立,则实数k的取值范围是( )
|
| A、[-1,-1] | ||||
| B、[-2,0] | ||||
C、[-
| ||||
D、[-
|
若An3=12Cn2,则n等于( )
| A、8 | B、4 | C、3或4 | D、5或6 |
下列图象中最左边是高青到张店71路公共汽车收支差额y与乘客量x的图象,则图①图②图③的实线所表达的实际意义是( )
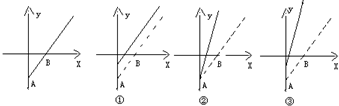

| A、①是票价不变降低成本,②是成本不变提高票价,③是降低成本提高票价 |
| B、①是成本不变提高票价,②是票价不变降低成本,③是降低成本提高票价 |
| C、①是降低成本提高票价,②是票价不变降低成本,③是票价不变降低成本 |
| D、①是成本不变提高票价,②是降低成本提高票价,③是降低成本提高票价 |
函数f(x)=log3x+2x-6的零点位于区间( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
圆x2+y2+2x+4y-3=1到直线x+y+1=0距离为
的点共有( )
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |