题目内容
已知定义域为[0,1]的函数f(x)同时满足:①f(1)=3;②f(x)≥2恒成立;③若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-2.
(1)求f(x)的最大值和最小值;
(2)试比较f(
)与
+2的大小(n∈N);
(3)若对任意x∈(0,1],总存在n(n∈N),使得
<x≤
,求证:对任意x∈(0,1],都有f(x)≤2x+2.
(1)求f(x)的最大值和最小值;
(2)试比较f(
| 1 |
| 2n |
| 1 |
| 2n |
(3)若对任意x∈(0,1],总存在n(n∈N),使得
| 1 |
| 2n+1 |
| 1 |
| 2n |
考点:数列与不等式的综合
专题:综合题,不等式的解法及应用
分析:(1)对于抽象函数的最值问题,可考虑此函数的单调性;
(2)由题中条件:f(x1+x2)≥f(x1)+f(x2)-2,令x1=x2=
,得f(
+
)≥f(
)+f(
)-2.即f(
)≥2f(
)-2,利用它进行放缩,可证得答案;
(3)利用f(x)≤f(
)≤
+2,即可证明.
(2)由题中条件:f(x1+x2)≥f(x1)+f(x2)-2,令x1=x2=
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n-1 |
| 1 |
| 2n |
(3)利用f(x)≤f(
| 1 |
| 2n |
| 1 |
| 2n |
解答:
(1)解:任取0≤x1<x2≤1,则0<x2-x1<1,且f(x2-x1)≥2.
于是f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)-2.
所以f(x2)-f(x1)≥f(x2-x1)-2≥0.
所以f(x2)≥f(x1).所以f(0)≤f(x)≤f(1).
由③,取x1=x2=0,得f(0)≤2;由②,得f(0)≥2;
所以f(0)=2.又f(1)=3,
所以,f(x)的最小值为2,最大值为3.…(4分)
(2)解:在③中,令x1=x2=
,得f(
+
)≥f(
)+f(
)-2.
即f(
)≥2f(
)-2,变形为f(
)-2≤
[f(
)-2].
于是f(
)-2≤
[f(
)-2]≤
[f(
)-2]≤…≤
[f(
)-2]=
,
所以f(
)≤
+2.…(9分)
(3)证明:对任意满足x∈(0,1],总存在n(n∈N),使得
<x≤
.
于是f(x)≤f(
)≤
+2,
又2x+2>2×
+2=
+2,
所以f(x)≤2x+2.…(14分)
于是f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)-2.
所以f(x2)-f(x1)≥f(x2-x1)-2≥0.
所以f(x2)≥f(x1).所以f(0)≤f(x)≤f(1).
由③,取x1=x2=0,得f(0)≤2;由②,得f(0)≥2;
所以f(0)=2.又f(1)=3,
所以,f(x)的最小值为2,最大值为3.…(4分)
(2)解:在③中,令x1=x2=
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
即f(
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2n-1 |
于是f(
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
| 1 |
| 2n |
| 1 |
| 20 |
| 1 |
| 2n |
所以f(
| 1 |
| 2n |
| 1 |
| 2n |
(3)证明:对任意满足x∈(0,1],总存在n(n∈N),使得
| 1 |
| 2n+1 |
| 1 |
| 2n |
于是f(x)≤f(
| 1 |
| 2n |
| 1 |
| 2n |
又2x+2>2×
| 1 |
| 2n+1 |
| 1 |
| 2n |
所以f(x)≤2x+2.…(14分)
点评:本题考查了抽象函数的性质,抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.抽象函数的抽象性赋予它丰富的内涵和多变的思维价值,可以考查类比猜测,合情推理的探究能力和创新精神.

练习册系列答案
相关题目
设数列{an}满足a1=0,an+an+1=2,则a2014的值为( )
| A、2 | B、1 | C、0 | D、-2 |
a>b>0,下列不等式一定成立的是( )
A、a+
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在平面直角坐标系xOy中,点A(x1,y1)在单位圆O上,∠xOA=α,且α∈(
如图,在平面直角坐标系xOy中,点A(x1,y1)在单位圆O上,∠xOA=α,且α∈(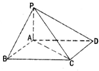 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,BC=2AB,PA⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,BC=2AB,PA⊥底面ABCD.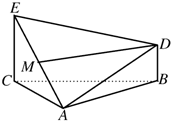 如图所示,已知△ABC是等边三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、DB在平面ABC的同侧,M为EA的中点,CE=2BD.
如图所示,已知△ABC是等边三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、DB在平面ABC的同侧,M为EA的中点,CE=2BD.