题目内容
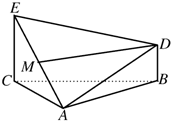 如图所示,已知△ABC是等边三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、DB在平面ABC的同侧,M为EA的中点,CE=2BD.
如图所示,已知△ABC是等边三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、DB在平面ABC的同侧,M为EA的中点,CE=2BD.(Ⅰ)求证:MD∥面ABC;
(Ⅱ)求证:平面DEA⊥平面ECA.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取AC中点N,连结MN、BN,由已知条件推导出四边形MNBD是平行四边形,由此能证明MD∥面ABC.
(Ⅱ)由已知条件推导出平面AEC⊥平面ABC,从而得到BN⊥平面ECA,由此能证明平面DEA⊥平面ECA.
(Ⅱ)由已知条件推导出平面AEC⊥平面ABC,从而得到BN⊥平面ECA,由此能证明平面DEA⊥平面ECA.
解答:
(本小题满分12分)
(Ⅰ)证明:如图,取AC中点N,连结MN、BN,
∵EC⊥平面ABC,BD⊥平面ABC,∴EC∥BD.…(2分)
△ECA中,M、N分别是EA、CA中点,∴MN∥EC,
且MN=
EC.又∵EC=2BD,∴MN∥BD且MN=BD.
∴四边形MNBD是平行四边形.…(4分)
∴MD∥BN.,又MD?面ABC,BN?面ABC,
∴MD∥面ABC;…(6分)
(Ⅱ)证明:∵正三角形ABC中,N是AC中点,
∴BN⊥AC.…(8分)
又∵EC⊥平面ABC,平面AEC⊥平面ABC,
且交线为AC,BN?面ABC,∴BN⊥平面ECA.…(10分)
而MD∥BN.∴MD⊥平面ECA,
∵MD⊆面AED,∴平面DEA⊥平面ECA.…(12分)

(Ⅰ)证明:如图,取AC中点N,连结MN、BN,
∵EC⊥平面ABC,BD⊥平面ABC,∴EC∥BD.…(2分)
△ECA中,M、N分别是EA、CA中点,∴MN∥EC,
且MN=
| 1 |
| 2 |
∴四边形MNBD是平行四边形.…(4分)
∴MD∥BN.,又MD?面ABC,BN?面ABC,
∴MD∥面ABC;…(6分)
(Ⅱ)证明:∵正三角形ABC中,N是AC中点,
∴BN⊥AC.…(8分)
又∵EC⊥平面ABC,平面AEC⊥平面ABC,
且交线为AC,BN?面ABC,∴BN⊥平面ECA.…(10分)
而MD∥BN.∴MD⊥平面ECA,
∵MD⊆面AED,∴平面DEA⊥平面ECA.…(12分)
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
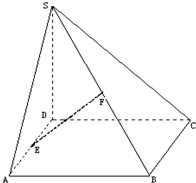 已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点,
已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点,