题目内容
下列有四种说法
①若复数z满足方程z2+2=0,则z3=-2
i;
②线性回归方程对应的直线y=bx+a一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
③若(1-2x)2012=a0+a1x+…a2012x2012(x∈R),则
+
+…+
=-1;
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
其中正确的是( )
①若复数z满足方程z2+2=0,则z3=-2
| 2 |
②线性回归方程对应的直线y=bx+a一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
③若(1-2x)2012=a0+a1x+…a2012x2012(x∈R),则
| a1 |
| 2 |
| a2 |
| 22 |
| a2012 |
| 22012 |
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
其中正确的是( )
| A、①② | B、③ | C、③④ | D、④ |
考点:命题的真假判断与应用,线性回归方程,二项式定理的应用
专题:阅读型,数系的扩充和复数,二项式定理
分析:①可先求出z,注意两解,然后计算z3;②由线性回归方程对应的直线的特点,即可判断;③可通过赋值法,分别令x=0,x=
,即可判断;④分别写出n=k,n=k+1的等式,对照比较左边即可判断④.
| 1 |
| 2 |
解答:
解:①若复数z满足方程z2+2=0,则z=±
i,z3=±2
i,故①错;
②线性回归方程对应的直线y=bx+a是由最小二乘法计算出来的,它不一定经过其样本数据点,
一定经过点(
,
),故②错;
③由于(1-2x)2012=a0+a1x+…a2012x2012(x∈R),可令x=
,则0=a0+
+
+…+
,
再令x=0,则a0=1,故
+
+…+
=-1,故③正确;
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,
当n=k时,为(k+1)(k+2)…(k+k)=2k•1•3…(2k-1),
当n=k+1时,应为(k+2)(k+3)…(k+k)(k+k+1)(k+k+2)=2k+1•1•3…(2k+1),
对照比较左边,左边需增添的一个因式是2(2k+1),故④正确.
故选C.
| 2 |
| 2 |
②线性回归方程对应的直线y=bx+a是由最小二乘法计算出来的,它不一定经过其样本数据点,
一定经过点(
. |
| x |
. |
| y |
③由于(1-2x)2012=a0+a1x+…a2012x2012(x∈R),可令x=
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a2012 |
| 22012 |
再令x=0,则a0=1,故
| a1 |
| 2 |
| a2 |
| 22 |
| a2012 |
| 22012 |
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,
当n=k时,为(k+1)(k+2)…(k+k)=2k•1•3…(2k-1),
当n=k+1时,应为(k+2)(k+3)…(k+k)(k+k+1)(k+k+2)=2k+1•1•3…(2k+1),
对照比较左边,左边需增添的一个因式是2(2k+1),故④正确.
故选C.
点评:本题以命题的真假判断为载体,考查复数的运算,线性回归方程对应直线的特点,解决二项式展开式的系数和问题常采用的赋值法,以及数学归纳法的运用,是一道基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
知向量
、
、
中任意二个都不共线,但
+
与
共线,且
+
与
共线,则向量
+
+
=( )
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| a |
| a |
| b |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=
f′(-1)x2-2x+3,则f′(-1)的值为( )
| 1 |
| 2 |
| A、0 | B、-1 | C、1 | D、2 |
已知sin2α=
,则cos2(α-
)=( )
| 1 |
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
复数z=(m-1)(m-8)+
ilog2m(m∈R)是纯虚数,则
=( )
| 1 |
| 3 |
| 1 |
| 1-z |
| A、1+i | ||||
| B、1-i | ||||
C、
| ||||
D、
|
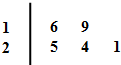 学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )
学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )| A、21和10.8 |
| B、24和10.8 |
| C、25和9.2 |
| D、5和9.2 |
(x2-1)(
-2)5的展开式的常数项是( )
| 1 |
| x |
| A、48 | B、-48 |
| C、112 | D、-112 |
