题目内容
（x2-1）（
-2）5的展开式的常数项是（ ）
| 1 |
| x |
| A、48 | B、-48 |
| C、112 | D、-112 |
考点：二项式系数的性质
专题：计算题,二项式定理
分析：第一个因式取x2，第二个因式取
；第一个因式取-1，第二个因式取（-2）5，即可得出结论．
| 1 |
| x2 |
解答：
解：第一个因式取x2，第二个因式取
，可得
•(-2)3=-80；
第一个因式取-1，第二个因式取（-2）5，可得（-1）×（-2）5=32
∴（x2-1）（
-2）5的展开式的常数项是-80+32=-48．
故选：B．
| 1 |
| x2 |
| C | 3 5 |
第一个因式取-1，第二个因式取（-2）5，可得（-1）×（-2）5=32
∴（x2-1）（
| 1 |
| x |
故选：B．
点评：本题考查二项式定理的运用，解题的关键是确定展开式的常数项得到的途径．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
在△ABC中，若cosA=
，AB：AC=3：2，则sinB的值为（ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知圆C1：(x+1)2+(y-1)2=1，圆C2与圆C1关于直线x-y=0对称，则圆C2的方程为（ ）
| A、（x-1）2+（y+1）2=1 |
| B、（x-1）2+（y-1）2=1 |
| C、（x+1）2+（y+1）2=1 |
| D、（x+1）2+（y-1）2=1 |
若不等式mx2+mnx+n＞0的解集为{x|1＜x＜2}，则m+n的值为（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知△ABC中，AB=
，BC=1，sinC=
cosC，则△ABC的面积为（ ）
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设z=1-i（i是虚数单位），则复数
+i2的实部是（ ）
| 3 |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
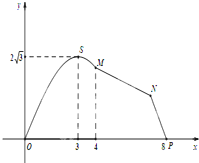如图，某市拟在长为8km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y=Asin（ωx）（A＞0，ω＞0），x∈[0，4]的图象，且图象的最高点为S（3，2