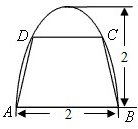
题目内容
用一根长为10m的绳索围成一个圆心角为α（0＜α＜π），半径不超过2m的扇形场地，设扇形的半径为x m，面积为S m2．
（1）写出S关于x的表达式，并求出此函数的定义域
（2）当半径x和圆心角α分别是多少时，所围成的扇形场地的面积S最大，并求最大面积．
（1）写出S关于x的表达式，并求出此函数的定义域
（2）当半径x和圆心角α分别是多少时，所围成的扇形场地的面积S最大，并求最大面积．
考点：扇形面积公式,基本不等式
专题：三角函数的求值
分析：（1）直接利用扇形的周长公式以及面积公式写出S关于x的表达式，并求出此函数的定义域．
（2）利用二次函数的单调性求出当半径x和圆心角α分别是多少时，所围成的扇形场地的面积S最大，直接求最大面积．
（2）利用二次函数的单调性求出当半径x和圆心角α分别是多少时，所围成的扇形场地的面积S最大，直接求最大面积．
解答：
解：（1）扇形的半径为x m，扇形的周长10m，
扇形的弧长为：10-2x，m
∴S=
（10-2x）x=-x2+5x，x∈（
，2]．
（2）∵S=-x2+5x，x∈（
，2]．函数S在x∈（
，2]上是增函数，
∴x=2时扇形面积最大，此时扇形的圆心角：
=3，
扇形面积的最大值为：6m2．
扇形的弧长为：10-2x，m
∴S=
| 1 |
| 2 |
| 10 |
| π+2 |
（2）∵S=-x2+5x，x∈（
| 10 |
| π+2 |
| 10 |
| π+2 |
∴x=2时扇形面积最大，此时扇形的圆心角：
| 6 |
| 2 |
扇形面积的最大值为：6m2．
点评：本题考查扇形面积公式以及周长公式的应用，二次函数的最大值的求法．
练习册系列答案
相关题目
若曲线y=x2+ax+b在点（1，b）处的切线方程是x-y+1=0，则（ ）
| A、a=1，b=2 |
| B、a=-1，b=2 |
| C、a=1，b=-2 |
| D、a=-1，b=-2 |
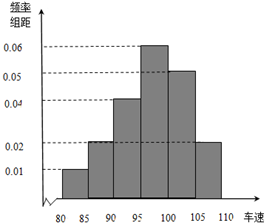2013年国庆期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段[80，85），[85，90），[90，95），[95，100），[100，105），[105，110）后得到如下图的频率分布直方图．
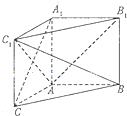如图，在直三棱柱ABC-A1B1C1中，AB⊥AC，且AB=AC=AA1=1．