题目内容
下列命题:
①若ac2>bc2,则a>b;
②若sinα=sinβ,则α=β;
③“实数a=0”是“直线x-2ay=1和直线2x-2ay=1平行”的充要条件;
④若f(x)=log2x,则f(|x|)是偶函数.
其中正确命题的序号是 .
①若ac2>bc2,则a>b;
②若sinα=sinβ,则α=β;
③“实数a=0”是“直线x-2ay=1和直线2x-2ay=1平行”的充要条件;
④若f(x)=log2x,则f(|x|)是偶函数.
其中正确命题的序号是
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:①可举反例,比如c为复数i,即可判断;②应用三角函数的定义,即可判断;③由两直线平行的条件判断,注意斜率不存在的情况;④根据函数的奇偶性定义即可判断,注意先判断定义域是否关于原点对称.
解答:
解:①由ac2>bc2,若c为实数,则a>b,若c为复数,比如c=i,则由ai2>bi2推出a<b,故①错;
②若sinα=sinβ,则α=2kπ+β或2kπ+π-β,k∈Z,故②不正确;
③由直线x-2ay=1和直线2x-2ay=1平行得,当斜率都不存在时,a=0,当斜率都存在,则
=
,a无解,故“实数a=0”是“直线x-2ay=1和直线2x-2ay=1平行”的充要条件,即③正确;
④若f(x)=log2x,则f(|x|)=log2|x|,首先定义域为{x|x≠0,x∈R},
f(|-x|)=log2|-x|=log2|x|=f(|x|),故f(|x|)是偶函数,故④正确.
故答案为:③④
②若sinα=sinβ,则α=2kπ+β或2kπ+π-β,k∈Z,故②不正确;
③由直线x-2ay=1和直线2x-2ay=1平行得,当斜率都不存在时,a=0,当斜率都存在,则
| 1 |
| 2a |
| 2 |
| 2a |
④若f(x)=log2x,则f(|x|)=log2|x|,首先定义域为{x|x≠0,x∈R},
f(|-x|)=log2|-x|=log2|x|=f(|x|),故f(|x|)是偶函数,故④正确.
故答案为:③④
点评:本题以命题的真假判断为载体,考查不等式的性质和两直线平行的条件,以及函数的奇偶性及应用,属于基础题.

练习册系列答案
相关题目
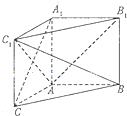 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,且AB=AC=AA1=1.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,且AB=AC=AA1=1.