题目内容
已知等差数列{an}和等比数列{bn}满足:a1=b1=1,a2=b2≠1,a5=b3,设cn=an+bn(n∈N*).
(1)求数列{cn}的通项公式;
(2)设Sn=c1+c2+c3+…+cn,求Sn的值.
(1)求数列{cn}的通项公式;
(2)设Sn=c1+c2+c3+…+cn,求Sn的值.
考点:数列的求和,等差数列的性质,等比数列的性质
专题:等差数列与等比数列
分析:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,依题意,可求得an=2n-1,bn=3n-1,从而可得数列{cn}的通项公式;
(2)Sn=c1+c2+c3+…+cn=(a1+a2+a3+…+an)+(b1+b2+b3+…+bn),利用分组求和法即可求得Sn的值.
(2)Sn=c1+c2+c3+…+cn=(a1+a2+a3+…+an)+(b1+b2+b3+…+bn),利用分组求和法即可求得Sn的值.
解答:
解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q(q≠1),
由已知得
,解得
,
所以an=2n-1,bn=3n-1,于是cn=(2n-1)+3n-1…(6分)
(2)Sn=c1+c2+c3+…+cn=(a1+a2+a3+…+an)+(b1+b2+b3+…+bn)
=(1+3+5+…+2n-1)+(1+3+32+…+3n-1)
=n2+
.…(12分)
由已知得
|
|
所以an=2n-1,bn=3n-1,于是cn=(2n-1)+3n-1…(6分)
(2)Sn=c1+c2+c3+…+cn=(a1+a2+a3+…+an)+(b1+b2+b3+…+bn)
=(1+3+5+…+2n-1)+(1+3+32+…+3n-1)
=n2+
| 3n-1 |
| 2 |
点评:本题考查数列的求和,着重考查等差数列与等比数列的通项公式的应用,考查分组求和法,属于中档题.

练习册系列答案
相关题目
若f(x)=sinα-cosx,则f′(α)等于( )
| A、sinα |
| B、cosα |
| C、2sinα |
| D、sinα+cosα |
已知sin(
+α)=
,则cos(α-
)=( )
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
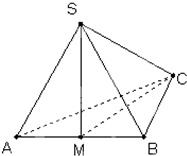 如图,在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
如图,在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
 已知:空间四边形ABCD中,E,F分别为BC,CD的中点,
已知:空间四边形ABCD中,E,F分别为BC,CD的中点,