题目内容
已知函数f(x)=
,若函数y=f2(x)-2bf(x)+b-
有6个零点,则b的取值范围是( )
|
| 2 |
| 9 |
A、[
| ||||||||
B、(
| ||||||||
C、(0,
| ||||||||
D、(
|
考点:分段函数的应用
专题:函数的性质及应用
分析:利用换元法将函数转化为关于t的一元二次函数,作出函数f(x)的图象,利用一元二次方程根的分布,建立不等式关系即可得到结论.
解答:
 解:设t=f(x),则函数等价为y=g(t)=t2-2bt+b-
解:设t=f(x),则函数等价为y=g(t)=t2-2bt+b-
.
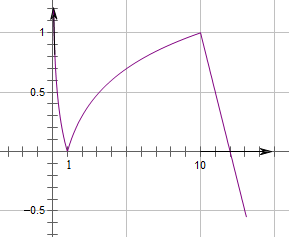
作出函数f(x)的图象如图:
当t>1或t<0时,t=f(x)有1个零点,
当t=1或t=0时,t=f(x)有2个零点,
当0<t<1时,t=f(x)有3个零点,
若函数y=f2(x)-2bf(x)+b-
有6个零点,等价为方程t2-2bt+b-
=0有两个根t1,t2,且0<t1<1,0<t2<1,
则
,即
,
解得
≤b<
或
<b≤
,
故选:A
 解:设t=f(x),则函数等价为y=g(t)=t2-2bt+b-
解:设t=f(x),则函数等价为y=g(t)=t2-2bt+b-| 2 |
| 9 |
作出函数f(x)的图象如图:
当t>1或t<0时,t=f(x)有1个零点,
当t=1或t=0时,t=f(x)有2个零点,
当0<t<1时,t=f(x)有3个零点,
若函数y=f2(x)-2bf(x)+b-
| 2 |
| 9 |
| 2 |
| 9 |
则
|
|
解得
| 2 |
| 3 |
| 7 |
| 9 |
| 2 |
| 9 |
| 1 |
| 3 |
故选:A
点评:本题主要考查分段函数的应用,利用换元法,结合一元二次函数图象和性质,利用数形结合是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
下列函数中,既是奇函数又是在定义域上是减函数的为( )
| A、y=x+1 | ||
B、y=
| ||
| C、y=-x3 | ||
| D、y=lnx |
|2x+2|-|2x-2|≤a能成立,则实数a的取值范围是( )
| A、(-∞,-4) |
| B、[4,+∞) |
| C、[-4,+∞) |
| D、(-4,+∞) |
已知x,y满足约束条件:x-2≤0,y-1≤0,-x-2y+2≤0,则z=-x-y的取值范围是( )
| A、[-3,-1] |
| B、[-2,-1] |
| C、[-3,-2] |
| D、[-3,+∞] |
对下列命题的否定错误的是( )
| A、p:2既是偶数又是素数;¬p:2不是偶数或不是素数 |
| B、p:至少有一个整数,它既不是合数,也不是素数;¬p:每一个整数,它是合数或素数 |
| C、p:?x∈N,x3>x2;¬p:?x∈N,x3≤x2 |
| D、p:负数的平方是正数;¬p:负数的平方不是正数 |
设P和Q是两个集合,定义集合P-Q={x|x∈P,且x∉Q},若Q={x|1<x<2},P={x|1<x<3},那么P-Q等于( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|1≤x<2} |
| D、{x|2≤x<3} |