题目内容
14.种子发芽率与昼夜温差有关.某研究性学习小组对此进行研究,他们分别记录了3月12日至3月16日的昼夜温差与每天100颗某种种子浸泡后的发芽数,如表:| 日 期 | 3月12日 | 3月13日 | 3月14日 | 3月15日 | 3月16日 |
| 昼夜温差(°C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数(颗) | 23 | 25 | 30 | 26 | 16 |
(II)请根据3月13日至3月15日的三组数据,求出y关于x的线性回归方程$\widehaty=\widehata+\widehatbx$;
(III)若由线性回归方程得到的估计数据与实际数据误差均不超过2颗,则认为回归方程是可靠的,试用3月12日与16日的两组数据检验,(II)中的回归方程是否可靠?
分析 (I)采用列举的方式,即可求解.
(II)利用公式求出$\hat{b}$,$\hat{a}$,即可得出结论.
(III)把3月12日中的x=10和16日中的x=8带入计算,误差均不超过2颗,认为回归方程是可靠的,即可判断.
解答 解:(Ⅰ)从5天中任选2天,共有10个基本事件:(12日,13日),(12日,14日),(12日,15日),(12日,16日),(13日,14日),(13日,15日),(13日,16日),(14日,15日),(14日,16日),(15日,16日).
选出的二天种子发芽数均不小于25共有3个基本事件:(13日,14日),(13日,15日),(14日,15日).
∴事件“c,d均不小于25”的概率为$P=\frac{3}{10}$;
(Ⅱ)由表中数据可得$\overline x=\frac{11+13+12}{3}=12,\overline y=\frac{25+30+26}{3}=27$.
则$\sum_{i=1}^3{x_i}{y_i}-3\overline x\overline y$=25×11+30×13+26×12-3×27×12=5.
$\sum_{i=1}^{3}{x}_{i}^{2}$-3$\overline{x}$2=112+122+132-3×122=-28.
∴$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$=$-\frac{5}{28}$,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=27+$\frac{15}{7}$=29$\frac{1}{7}$;
故回归直线方程为$\widehat{y}$=$-\frac{5}{28}$x$+29\frac{1}{7}$.
(III)3月12日中的x=10时,可得:y≈28,误差不超过2颗.
16日中的x=8时,可得:y≈28,误差不超过2颗.
∴(II)中的回归方程不可靠.
点评 本题考查了线性回归方程的求法及应用,属于基础题.

 作业辅导系列答案
作业辅导系列答案| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $±\frac{3}{5}$ | D. | $±\frac{4}{5}$ |
| A. | (-2,-1) | B. | [-2,-1) | C. | (-2,+∞) | D. | [-2,+∞) |
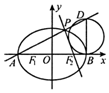 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点为F1,F2,点M为椭圆C上的任意一点,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点为F1,F2,点M为椭圆C上的任意一点,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2.