题目内容
计算:(0.064)
-(-
)0+[(-2)3]
+log28+|-0.01|
= .
| 1 |
| 3 |
| 7 |
| 8 |
| 4 |
| 3 |
| 1 |
| 2 |
考点:有理数指数幂的化简求值
专题:计算题,函数的性质及应用
分析:化0指数幂为1,运用有理指数幂的运算性质及对数的运算性质化简求值.
解答:
解:(0.064)
-(-
)0+[(-2)3]
+log28+|-0.01|
=[(0.4)3]
-1+(-2)4+log223+[(0.1)2]
=0.4-1+16+3+0.1
=18.5.
故答案为:18.5.
| 1 |
| 3 |
| 7 |
| 8 |
| 4 |
| 3 |
| 1 |
| 2 |
=[(0.4)3]
| 1 |
| 3 |
| 1 |
| 2 |
=0.4-1+16+3+0.1
=18.5.
故答案为:18.5.
点评:本题考查了有理指数幂的运算性质,考查了对数的运算性质,是基础的计算题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
函数f(x)的定义域为{x|x≠0},f(x)>0.满足f(x•y)=f(x)•f(y),且在区间(0,+∞)上单调递增,若实数a满足f(log2a)+f(log
a)≤2f(1),则a的取值范围是( )
| 1 |
| 2 |
| A、[1,2] | ||
B、(0,
| ||
C、[
| ||
| D、(0,1)∪(1,2] |
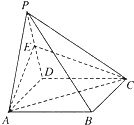 如图,已知正三角形PAD,正方形ABCD,平面PAD⊥平面ABCD,E为PD的中点.
如图,已知正三角形PAD,正方形ABCD,平面PAD⊥平面ABCD,E为PD的中点.