题目内容
14.已知f(x)=sinx(1+sin2x)+cosxcos2x+2-$\sqrt{2}$.若△ABC的内角A,B,C的对边分别为a,b,c,且满足a=b,$\frac{sin(2A+C)}{sinA}=\sqrt{2}-2cosB$.则f(B)的值为 ( )| A. | 2 | B. | $\frac{1}{2}$ | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 利用两角差的余弦公式将f(x)化简f(x)═$\sqrt{2}$sin(x+$\frac{π}{4}$)+2-$\sqrt{2}$,根据等腰三角形关系,2A+C=π,化简求得B=$\frac{π}{4}$,代入求得,f(B)=2.
解答 解:f(x)=sinx(1+sin2x)+cosxcos2x+2-$\sqrt{2}$,
=sinx+sinxsin2x+cosxcos2x+2-$\sqrt{2}$,
=cosx+sinx+2-$\sqrt{2}$,
=$\sqrt{2}$sin(x+$\frac{π}{4}$)+2-$\sqrt{2}$,
$\frac{sin(2A+C)}{sinA}=\sqrt{2}-2cosB$,
若△ABC的内角A,B,C的对边分别为a,b,c,且满足a=b,
∴A=B,A+B+C=π,
∴2A+C=π,
$\frac{sin[(A+C)+A]}{sinA}$=0,
∴$\sqrt{2}$-2cosB=0,cosB=$\frac{\sqrt{2}}{2}$,
∴B=$\frac{π}{4}$,
f(B)=f($\frac{π}{4}$)=$\sqrt{2}$+2-$\sqrt{2}$=2,
∴f(B)=2,
故答案选:A.
点评 本题考查两角差的余弦公式和等腰三角形的性质,属于中档题.

练习册系列答案
相关题目
19.A,B,C,D,E五人并排站成-行,如果A,B必须相邻且B在A的右边.耶么不同的排法种数是( )
| A. | 6 | B. | 24 | C. | 48 | D. | 120 |
6.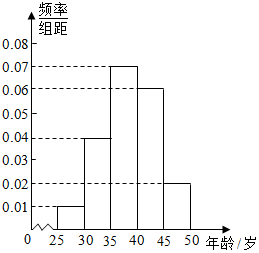 某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:
某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:
(1)求频数分布表中x,y的值;
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加iphone手机宣传活动,现从这20人中随机选取2人各赠送一部iphone6s手机,设这2名市民中年龄在[40,45)内的人数为X,求X的分布列及数学期望.
 某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:
某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:| 分组(岁) | 频数 |
| [25,30) | 5 |
| [30,35) | x |
| [35,40) | 35 |
| [40,45) | y |
| [45,50] | 10 |
| 合计 | 100 |
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加iphone手机宣传活动,现从这20人中随机选取2人各赠送一部iphone6s手机,设这2名市民中年龄在[40,45)内的人数为X,求X的分布列及数学期望.
4.M={x|5-x≥$\sqrt{2(x-1)}$},N={x|x2-ax≤x-a},当M?N时,a的取值范围是( )
| A. | a≥3 | B. | a≤3 | C. | a<3 | D. | a>3 |