题目内容
19.A,B,C,D,E五人并排站成-行,如果A,B必须相邻且B在A的右边.耶么不同的排法种数是( )| A. | 6 | B. | 24 | C. | 48 | D. | 120 |
分析 根据题意,A、B必须相邻且B在A的右边,视A、B为一个元素,且只有一种排法;将A、B与其他3个元素,共4个元素排列,由乘法计数原理可得答案
解答 解:根据题意,A、B必须相邻且B在A的右边,视A、B为一个元素,且只有一种排法;
将A、B与其他3个元素,共4个元素排列,
即A44=24,
则符合条件的排法有1×24=24种;
故选B.
点评 本题考查排列的运用,注意分析相邻问题时,要用捆绑法.

练习册系列答案
相关题目
9.已知i是虚数单位,若复数z1=3-i,z2=1-i,则z1•$\overline{{z}_{2}}$=4+2i,$\frac{{z}_{1}}{{z}_{2}}$在复平面内所对应的点位于第一象限.
14.已知f(x)=sinx(1+sin2x)+cosxcos2x+2-$\sqrt{2}$.若△ABC的内角A,B,C的对边分别为a,b,c,且满足a=b,$\frac{sin(2A+C)}{sinA}=\sqrt{2}-2cosB$.则f(B)的值为 ( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
8.如图,已知直线y=kx+m与曲线y=f(x)相切于两点,则F(x)=f(x)-kx有( )
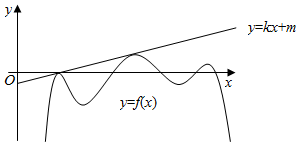

| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
9.对于锐角α,若sin(α-$\frac{π}{6}$)=$\frac{1}{3}$,则cos(α-$\frac{π}{3}$)=( )
| A. | $\frac{2\sqrt{6}+1}{6}$ | B. | $\frac{3-\sqrt{2}}{8}$ | C. | $\frac{3+\sqrt{2}}{8}$ | D. | $\frac{2\sqrt{3}-1}{6}$ |
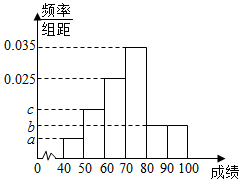 已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.
已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.