题目内容
9.有4位男学生3位女生排队拍照,根据下列要求,各有多少种不同的排列结果?(1)4个男学生必须连在一起;
(2)其中甲、乙两人之间必须间隔2人;
(3)若三女生互不相邻;
(4)若甲、乙两位同学必须排两端;
(5)若甲、乙两位同学不得排两端
(6)若甲、乙两女生相邻且不与第三女生相邻.
分析 根据特殊元素优先安排,相邻问题用捆绑,不相邻用插空法,即可求解.
解答 解:(1)男生必须排在一起把4名男生捆绑在一起看做一个复合元素,再和3位女生全排,故有A44A44=576种;
(2)甲、乙中间必须有2人,从5人选2人和甲乙捆绑在一起,再和另外3人全排列,故有A52A22A44=960种;
(3)三女生互不相邻,先排男生形成了5个空中,插入3名女生,故有A44A53=1440种;
(4)甲、乙必须在两端;A22A55=240种
(5)甲、乙两位同学不得排两端,先从5人选2排在两端,剩下的全排,故有A52A55=2400种;
(6)把甲乙两位女生捆绑在一起和另一位女生插入到男生形成了5个空中,故有A22A44A52=690种.
点评 本题考查排列的应用,相邻问题一般看作一个整体处理,不相邻,用插空法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知f(x)=sinx(1+sin2x)+cosxcos2x+2-$\sqrt{2}$.若△ABC的内角A,B,C的对边分别为a,b,c,且满足a=b,$\frac{sin(2A+C)}{sinA}=\sqrt{2}-2cosB$.则f(B)的值为 ( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
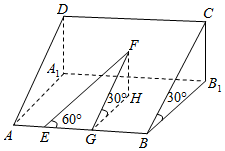 如图所示,山坡的倾角为30°(就是坡面AC与地平面AB1所成的二面角是30°),山坡上有一条与斜坡底线AB成60°角的小路EF,如果某人从点E开始沿这条小路走了40m,问此人离开地平面的高度约为多少米(精确到1m)?
如图所示,山坡的倾角为30°(就是坡面AC与地平面AB1所成的二面角是30°),山坡上有一条与斜坡底线AB成60°角的小路EF,如果某人从点E开始沿这条小路走了40m,问此人离开地平面的高度约为多少米(精确到1m)?