题目内容
3.已知Sn为数列{an}的前n项和,且S3=1,S4=11,an+3=2an(n∈N*),则S3n+1=3×2n+1-1.分析 S3=1,S4=11,可得a4=S4-S3.由于an+3=2an(n∈N*),可得:a3n+1=2a3n-2.数列{a3n-2}成等比数列,可得a3n-2=a4×2n-2,利用数列{S3n}成等比数列,即可得出.
解答 解:∵S3=1,S4=11,∴a4=S4-S3=10.
∵an+3=2an(n∈N*),∴a3n+1=2a3n-2.
数列{a3n-2}成等比数列,a4=10,公比为2.
∴a3n-2=a4×2n-2=10×2n-2.
∴数列{S3n}成等比数列,首项S3=1,公比为2.
则S3n+1=S3n+a3n+1=$\frac{{2}^{n}-1}{2-1}$+10×2n-1=3×2n+1-1.
故答案为:3×2n+1-1.
点评 本题考查了等比数列的通项公式性质及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.集合A={x||x|≤1},B={x∈Z|$\frac{1}{x}$≤1},则A∩B=( )
| A. | {-1,1} | B. | {0,1} | C. | {-1,0,1} | D. | {1} |
14.已知f(x)=sinx(1+sin2x)+cosxcos2x+2-$\sqrt{2}$.若△ABC的内角A,B,C的对边分别为a,b,c,且满足a=b,$\frac{sin(2A+C)}{sinA}=\sqrt{2}-2cosB$.则f(B)的值为 ( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
8.如图,已知直线y=kx+m与曲线y=f(x)相切于两点,则F(x)=f(x)-kx有( )
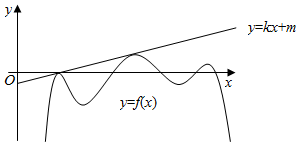

| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
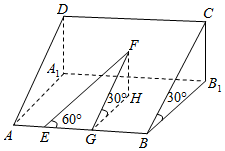 如图所示,山坡的倾角为30°(就是坡面AC与地平面AB1所成的二面角是30°),山坡上有一条与斜坡底线AB成60°角的小路EF,如果某人从点E开始沿这条小路走了40m,问此人离开地平面的高度约为多少米(精确到1m)?
如图所示,山坡的倾角为30°(就是坡面AC与地平面AB1所成的二面角是30°),山坡上有一条与斜坡底线AB成60°角的小路EF,如果某人从点E开始沿这条小路走了40m,问此人离开地平面的高度约为多少米(精确到1m)?