题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≥0}\\{1,x<0}\end{array}\right.$.(1)写出该函数的单调递增区间;
(2)解不等式f(1-x2)>f(2x).
分析 (1)根据二次函数的单调性便可得出该函数的单调递增区间为[0,+∞);
(2)根据f(x)的解析式可讨论x:①$\left\{\begin{array}{l}{1-{x}^{2}≥0}\\{2x≥0}\end{array}\right.$,根据f(x)的单调性,从而有1-x2>2x,这样便可得到$0≤x<-1+\sqrt{2}$,②$\left\{\begin{array}{l}{1-{x}^{2}>0}\\{2x<0}\end{array}\right.$,这种情况满足f(1-x2)>f(2x),从而便可得出原不等式的解集.
解答 解:(1)x≥0时,f(x)=x2+1单调递增;
∴f(x)的单调递增区间为[0,+∞);
(2)①若$\left\{\begin{array}{l}{1-{x}^{2}≥0}\\{2x≥0}\end{array}\right.$,即0≤x≤1,则1-x2>2x;
解得$-1-\sqrt{2}<x<-1+\sqrt{2}$;
∴$0≤x<-1+\sqrt{2}$;
②若$\left\{\begin{array}{l}{1-{x}^{2}>0}\\{2x<0}\end{array}\right.$,即-1<x<0,满足f(1-x2)>f(2x);
∴综上得原不等式的解集为$(-1,-1+\sqrt{2})$.
点评 考查二次函数的单调性,分段函数单调性的判断,以及根据函数的单调性解不等式.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
19.已知θ是△ABC的一个内角,且sinθ+cosθ=$\frac{3}{4}$,则方程x2sinθ-y2cosθ=1表示( )
| A. | 焦点在x轴上的双曲线 | B. | 焦点在y轴上的双曲线 | ||
| C. | 焦点在x轴上的椭圆 | D. | 焦点在y轴上的椭圆 |
13.已知函数f(x)=$\left\{\begin{array}{l}\frac{1}{x}+1,0<x≤2\\ lnx,\;\;x>2\end{array}$,如果关于x的方程f(x)=k有两个不同的实根,那么实数k的取值范围是( )
| A. | (1,+∞) | B. | $[\frac{3}{2},+∞)$ | C. | $[{e^{\frac{3}{2}}},+∞)$ | D. | [ln2,+∞) |
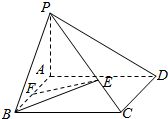 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,且BE⊥PC于E,PA=a,$BE=\frac{{\sqrt{6}}}{3}a$,点F在线段AB上,并有EF∥平面PAD.则$\frac{BF}{FA}$=$\frac{1}{2}$.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,且BE⊥PC于E,PA=a,$BE=\frac{{\sqrt{6}}}{3}a$,点F在线段AB上,并有EF∥平面PAD.则$\frac{BF}{FA}$=$\frac{1}{2}$.