题目内容
求到定点A(2,0)的距离与直线x=4的距离之比为
的动点的轨迹方程,并说明曲线的形状.
| ||
| 2 |
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:设出动点坐标,由题意列出关系式,代入点的坐标求得动点的轨迹方程.
解答:
解:设动点为M,坐标为(x,y),
再设动点M到直线x=4的距离为d,
由题意得:
=
,即
=
,
整理得:
+
=1.
∴动点的轨迹是焦点在x轴上的椭圆.
再设动点M到直线x=4的距离为d,
由题意得:
| |MA| |
| d |
| ||
| 2 |
| ||
| |x-4| |
| ||
| 2 |
整理得:
| x2 |
| 8 |
| y2 |
| 4 |
∴动点的轨迹是焦点在x轴上的椭圆.
点评:本题考查了椭圆的定义,考查了利用求轨迹方程的方法求椭圆的方程,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列结论中正确的是( )
| A、偶函数的图象一定与y轴相交 |
| B、奇函数y=f(x)在x=0处有定义,则f(0)=0 |
| C、奇函数y=f(x)图象一定过原点 |
| D、图象过原点的奇函数必是单调函数 |
双曲线
-
=-1与抛物线y=
x2有一个公共焦点F,双曲线上过点F且垂直实轴的弦长为
,则双曲线的离心率等于( )
| x2 |
| b2 |
| y2 |
| a2 |
| 1 |
| 8 |
2
| ||
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
设集合M={x|x=
+
,k∈Z},N={x|x=
+
,k∈Z},则( )
| k |
| 2 |
| 1 |
| 2 |
| k |
| 4 |
| 1 |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
已知A(x1,y1),B(x2,y2)是直线ax+by+c=0(b≠0)上两点,则|AB|等于( )
A、
| ||||
B、|
| ||||
C、|x1-x2|•
| ||||
D、|
|
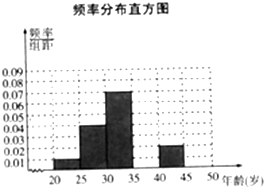 为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2
为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).