题目内容
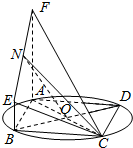 如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4
如图,已知AC,BD是圆O的两条互相垂直的直径,直角梯形ABEF所在平面与圆O所在平面互相垂直,其中∠FAB=∠EBA=90°,BE=2,AF=6,AC=4| 2 |
(Ⅰ)求证:直线NO∥平面EBC;
(Ⅱ)若点M在线段AC上,且点M在平面CEF上的射影为线段NC的中点,请求出线段AM的长.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)说明AF⊥平面ABCD,以点A为原点可建立空间直角坐标系,求出B,C,O,E,F,N的坐标,说明
=(4,0,0)是平面EBC的法向量,通过
•
=(4,0,0)•(0,2,-4)=0,证明直线NO∥平面EBC.(Ⅱ)点M在线段AC上,可设
=λ
=λ(4,4,0)=(4λ,4λ,0)
NC的中点为Q(3,2,2),
=(3-4λ,2-4λ,2),利用MQ⊥平面CEF,数量积为0,求出λ,然后求解线段AM的长.
| AB |
| AB |
| NO |
| AM |
| AC |
NC的中点为Q(3,2,2),
| MQ |
解答:
解:(Ⅰ)由题设AF⊥AB,且平面ABEF⊥平面ABCD,可知AF⊥平面ABCD
又BD是圆的直径,AB⊥AD,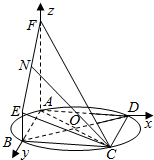
因此,以点A为原点可建立空间直角坐标系如图
由于AC,BD是圆O的两条互相垂直的直径,且AC=4
,
所以四边形ABCD是边长为4的正方形
则B(4,0,0),C(4,4,0),O(2,2,0),E(4,0,2),F(0,0,6),N(2,0,4)∵AB,⊥EB,AB,⊥BC,∴
=(4,0,0)是平面EBC的法向量∵
=(0,2,-4),
•
=(4,0,0)•(0,2,-4)=0
所以直线NO∥平面EBC …(7分)
(Ⅱ)点M在线段AC上,可设
=λ
=λ(4,4,0)=(4λ,4λ,0)
NC的中点为Q(3,2,2),
=(3-4λ,2-4λ,2),
由题设有MQ⊥平面CEF
∵
=(-4,0,4),
=(0,4,-2),
∴
解得λ=
=(4λ,4λ,0)=(1,1,0),
线段AM的长为|
|=
…(13分)
又BD是圆的直径,AB⊥AD,

因此,以点A为原点可建立空间直角坐标系如图
由于AC,BD是圆O的两条互相垂直的直径,且AC=4
| 2 |
所以四边形ABCD是边长为4的正方形
则B(4,0,0),C(4,4,0),O(2,2,0),E(4,0,2),F(0,0,6),N(2,0,4)∵AB,⊥EB,AB,⊥BC,∴
| AB |
| NO |
| AB |
| NO |
所以直线NO∥平面EBC …(7分)
(Ⅱ)点M在线段AC上,可设
| AM |
| AC |
NC的中点为Q(3,2,2),
| MQ |
由题设有MQ⊥平面CEF
∵
| EF |
| EC |
∴
|
解得λ=
| 1 |
| 4 |
| AM |
线段AM的长为|
| AM |
| 2 |
点评:本题考查空间直角坐标系的应用,向量的数量积证明直线与平面平行,直线与平面垂直的应用,考查空间两点间的距离公式的应用.

练习册系列答案
相关题目
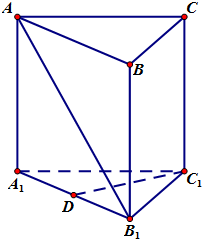 如图,直三棱柱ABC-A1B1C1中,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC=BC=| 2 |
| 3 |
(1)求证:C1D⊥AB1;
(2)若点F是BB1上的动点,求FB1的长度,使AB1⊥面C1DF.
设数列{an}满足an+an+1=3,且前三项之和S3=4,前四项之和S4=6,则a100=( )
| A、0 | B、1 | C、2 | D、3 |
下列四个图象中,两个变量具有正相关关系的是( )
A、 |
B、 |
C、 |
D、 |
