题目内容
现有红、黄、蓝、绿四种不同颜色的灯泡各一个，从中选取三个分别安装在△ABC的三个顶点处，则A处不安装红灯的概率为 ．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：先根据排列组合求出从中选取三个分别安装在△ABC的三个顶点处的种数，再求出A处不安装红灯的种数，根据概率公式计算即可．
解答：
解：红、黄、蓝、绿四种不同颜色的灯泡各一个，从中选取三个分别安装在△ABC的三个顶点处共有
=24种，
A处不安装红灯共有
•
=18种，
故A处不安装红灯的概率P=
=
．
故答案为：
．
| A | 3 4 |
A处不安装红灯共有
| A | 1 3 |
| A | 2 3 |
故A处不安装红灯的概率P=
| 18 |
| 24 |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题主要考查了排列组合的问题和古典概型的概率问题，属于基础题．
练习册系列答案
相关题目
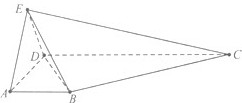如图所示，在四棱锥E-ABCD中，AB∥CD，∠ADC=90°，CD=3，AB=1，EA=AD=DE=2，EC=