题目内容
“求方程(
)x+(
)x的解”有如下解题思路:设f(x)=(
)x+(
)x,则f(x)在R上是单调递减函数,且f(2)=1,所以原方程有唯一解x=2.类比上述解题思路,不等式x3-
>(x+2)
-x的解集是 .
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| x+2 |
| 3 |
| 2 |
考点:类比推理
专题:
分析:把给出的不等式变形为x3+x>(x+2)
+
,然后引入函数f(x)=x3+x,由函数的单调性把不等式转化为较简单的不等式,然后求解即可.
| 3 |
| 2 |
| x+2 |
解答:
解:把不等式x3-
>(x+2)
-x变形,
可得x3+x>(x+2)
+
,
考查函数f(x)=x3+x,函数f(x)在R上为增函数,
故f(u)>f(v)?u>v;
不等式x3+x>(x+2)
+
中的x看作u,
看作v,
则有x>
,
解得x>2.
故答案为:{x|x>2}.
| x+2 |
| 3 |
| 2 |
可得x3+x>(x+2)
| 3 |
| 2 |
| x+2 |
考查函数f(x)=x3+x,函数f(x)在R上为增函数,
故f(u)>f(v)?u>v;
不等式x3+x>(x+2)
| 3 |
| 2 |
| x+2 |
| x+2 |
则有x>
| x+2 |
解得x>2.
故答案为:{x|x>2}.
点评:解答本题的关键是把复杂的高次不等式通过合理变化,转化为较简单的不等式,构造函数并且利用函数的单调性进行转化是解答本题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
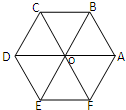 (1)如图,正六边形ABCDEF中,点O为其中心,以这七个点为起点与终点的向量中,与向量
(1)如图,正六边形ABCDEF中,点O为其中心,以这七个点为起点与终点的向量中,与向量 如图,斜边长为4的直角△ABC,∠B=90°,∠A=60°且A在平面α上,B、C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形△AB′C′,则M到平面α的距离的取值范围是
如图,斜边长为4的直角△ABC,∠B=90°,∠A=60°且A在平面α上,B、C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形△AB′C′,则M到平面α的距离的取值范围是