题目内容
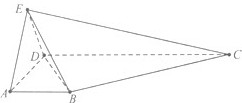 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=| 13 |
(Ⅰ)若F是线段DC上的点,DF=2FC,求证:AF∥平面EBC;
(Ⅱ)求三棱锥E-BDC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明四边形ABCF为平行四边形,可得AF∥BC,利用线面平行的判定定理,即可证明AF∥平面EBC;
(Ⅱ)取AD的中点H,连接EH、CH,证明EH⊥平面ABCD,即可求出求三棱锥E-BDC的体积.
(Ⅱ)取AD的中点H,连接EH、CH,证明EH⊥平面ABCD,即可求出求三棱锥E-BDC的体积.
解答:
 (I)证明:∵CD=3,DF=2FC,
(I)证明:∵CD=3,DF=2FC,
∴FC=AB=1,又∵AB∥CD,
∴四边形ABCF为平行四边形.…(2分)
∴AF∥BC,
又∵AF?平面EBC,BC?平面EBC,
∴AF∥平面EBC.…(5分)
(II)解:取AD的中点H,连接EH、CH.
∵EA=AD=DE=2,∴△ADE为正三角形,
∴EH⊥AD,EH=
.…(6分)
在Rt△HDC中,CD=3,DH=1,
∴HC=
=
=
,
在△EHC中,EH=
,HC=
,EC=
,∴EC2=EH2+HC2,∴∠EHC=90°,EH⊥HC.…(8分)
又∵AD?平面ABCD,HC?平面ABCD,AD∩HC=H,∴EH⊥平面ABCD,…(10分)
∵S△BCD=
×DC×AD=
×3×2=3,
故VE-BCD=
×S△BCD×EH=
×3×
=
.…(12分)
 (I)证明:∵CD=3,DF=2FC,
(I)证明:∵CD=3,DF=2FC,∴FC=AB=1,又∵AB∥CD,
∴四边形ABCF为平行四边形.…(2分)
∴AF∥BC,
又∵AF?平面EBC,BC?平面EBC,
∴AF∥平面EBC.…(5分)
(II)解:取AD的中点H,连接EH、CH.
∵EA=AD=DE=2,∴△ADE为正三角形,
∴EH⊥AD,EH=
| 3 |
在Rt△HDC中,CD=3,DH=1,
∴HC=
| CD2+DH2 |
| 32+12 |
| 10 |
在△EHC中,EH=
| 3 |
| 10 |
| 13 |
又∵AD?平面ABCD,HC?平面ABCD,AD∩HC=H,∴EH⊥平面ABCD,…(10分)
∵S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
故VE-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评:熟练掌握平行四边形的判定和性质定理、线面平行的判定定理与线面、及三棱锥体积的求法是解题的关键.

练习册系列答案
相关题目
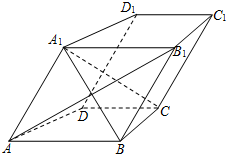 如图,在四棱柱ABCD-A1B1C1D1中,AB1⊥BC,AB∥CD,BC⊥AB且AA1=AB=AD=2,∠A1AB=∠DAB=60°.
如图,在四棱柱ABCD-A1B1C1D1中,AB1⊥BC,AB∥CD,BC⊥AB且AA1=AB=AD=2,∠A1AB=∠DAB=60°.