题目内容
已知函数f（x）=2cos2x+2sinxcosx．
（Ⅰ）求f（
）的值；
（Ⅱ）记函数g（x）=f（x-
）•f（x+
），若x∈[
，
]，求函数g（x）的值域．
（Ⅰ）求f（
| π |
| 12 |
（Ⅱ）记函数g（x）=f（x-
| π |
| 4 |
| π |
| 4 |
| π |
| 12 |
| π |
| 3 |
考点：三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：（Ⅰ）化简可得f（x）=1+cos2x+sin2x，代值计算可得；（Ⅱ）化简可得g（x）=sin4x，由x的范围和三角函数的性质可得值域．
解答：
解：（Ⅰ）化简可得f（x）=2cos2x+2sinxcosx=1+cos2x+sin2x
∴f（
）=1+cos
+sin
=1+
+
=1+
；
（Ⅱ）g（x）=f（x-
）•f（x+
）
=（1+sin2x-cos2x）（1-sin2x+cos2x）
=1-（sin2x-cos2x）2=2sin2xcos2x=sin4x，
∵x∈[
，
]，∴4x∈[
，
]，
∴g（x）=sin4x∈[-
，1]
∴函数g（x）的值域为：[-
，1]
∴f（
| π |
| 12 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
1+
| ||
| 2 |
（Ⅱ）g（x）=f（x-
| π |
| 4 |
| π |
| 4 |
=（1+sin2x-cos2x）（1-sin2x+cos2x）
=1-（sin2x-cos2x）2=2sin2xcos2x=sin4x，
∵x∈[
| π |
| 12 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴g（x）=sin4x∈[-
| ||
| 2 |
∴函数g（x）的值域为：[-
| ||
| 2 |
点评：本题考查三角函数的图象和性质，属基础题．
练习册系列答案
相关题目
实数x，y满足
，求目标函数z=-x+y的最小值（ ）
|
| A、1 | B、0 | C、-3 | D、5 |
阅读程序框图，执行相应的程序，若输入x=4，则输出y的值为（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
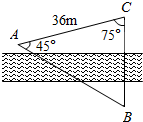如图，在一次测量活动中，要测量河两岸B、C两点间的距离，测量者在河的一侧测得AC=36m，∠BAC=45°，∠BCA=75°，求B、C两点之间的距离．