题目内容
18.已知$\overrightarrow a=({sinx,\sqrt{3}cosx})$,$\overrightarrow b=({cosx,-cosx})$,函数f(x)=$\overrightarrow a•\overrightarrow b+\frac{{\sqrt{3}}}{2}$.(Ⅰ)求函数y=f(x)图象的对称轴方程;
(Ⅱ)若方程f(x)=$\frac{1}{3}$在(0,π)上的解为x1,x2,求cos(x1-x2)的值.
分析 (Ⅰ)由已知利用平面向量数量积的运算,三角函数恒等变换的应用化简可得函数解析式为f(x)=sin(2x-$\frac{π}{3}$),利用正弦函数的对称性即可得解.
(Ⅱ)由条件知$sin({2{x_1}-\frac{π}{3}})=sin({2{x_2}-\frac{π}{3}})=\frac{1}{3}>0$,且$0<{x_1}<\frac{5π}{12}<{x_2}<\frac{2π}{3}$,可求${x_1}+{x_2}=\frac{5π}{6}$,利用诱导公式即可化简求值得解.
解答 解:(Ⅰ)$f(x)=\overrightarrow a•\overrightarrow b+\frac{{\sqrt{3}}}{2}=({sinx,\sqrt{3}cosx})•({cosx,-cosx})+\frac{{\sqrt{3}}}{2}$
=$sinx•cosx-\sqrt{3}{cos^2}x+\frac{{\sqrt{3}}}{2}=\frac{1}{2}sin2x-\frac{{\sqrt{3}}}{2}cos2x=sin({2x-\frac{π}{3}})$,
令$2x-\frac{π}{3}=kπ+\frac{π}{2}$,得$x=\frac{5π}{12}+\frac{k}{2}π({k∈Z})$,
即y=f(x)的对称轴方程为$x=\frac{5π}{12}+\frac{k}{2}π$,(k∈Z).
(Ⅱ)由条件知$sin({2{x_1}-\frac{π}{3}})=sin({2{x_2}-\frac{π}{3}})=\frac{1}{3}>0$,且$0<{x_1}<\frac{5π}{12}<{x_2}<\frac{2π}{3}$,
易知(x1,f(x1))与(x2,f(x2))关于$x=\frac{5π}{12}$对称,则${x_1}+{x_2}=\frac{5π}{6}$,
∴$cos({{x_1}-{x_2}})=cos[{{x_1}-({\frac{5π}{6}-{x_1}})}]=cos({2{x_1}-\frac{5π}{6}})=cos{[{({2{x_1}-\frac{π}{3}})-\frac{π}{2}}]}=sin({2{x_1}-\frac{π}{3}})=\frac{1}{3}$.
点评 本题主要考查了平面向量数量积的运算,三角函数恒等变换的应用,正弦函数的对称性的综合应用,考查了数形结合思想和转化思想,属于中档题.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案| A. | 1 | B. | -1 | C. | $-\frac{1}{2}$ | D. | 2 |
| A. | 2 | B. | $2\sqrt{3}$ | C. | 3 | D. | $2\sqrt{5}$ |
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=6x |
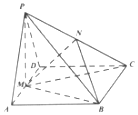 已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P的底面ABCD的射影,N是PC的中点.
已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P的底面ABCD的射影,N是PC的中点.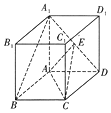 如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上,且E为A1D的中点
如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上,且E为A1D的中点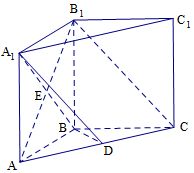 如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;
如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;