题目内容
9.已知圆心在x轴上,半径为$\sqrt{5}$的圆位于y轴右侧,且截直线x+2y=0所得弦的长为2,则圆的方程为(x-2$\sqrt{5}$)2+y2=5.分析 根据题意,设圆的圆心的坐标为(a,0),则圆的方程为(x-a)2+y2=5,(a>0),由点到直线的距离公式计算可得圆心到直线x+2y=0的距离,由此可得1+($\frac{\sqrt{5}}{5}$a)2=5,解可得a的值,将a的值代入圆的方程可得答案.
解答 解:根据题意,设圆的圆心坐标为(a,0),则其标准方程为(x-a)2+y2=5,(a>0),
则圆心到直线x+2y=0的距离d=$\frac{|a+2×0|}{\sqrt{1+{2}^{2}}}$=$\frac{\sqrt{5}}{5}$a,
又由该圆截直线x+2y=0所得弦的长为2,
则有1+($\frac{\sqrt{5}}{5}$a)2=5,
解可得a=±2$\sqrt{5}$,
又由a>0,则a=2$\sqrt{5}$,
故要求圆的方程为(x-2$\sqrt{5}$)2+y2=5,
故答案为:(x-2$\sqrt{5}$)2+y2=5.
点评 本题考查圆的标准方程,关键是依据题意,设出圆的圆心的坐标,得到圆的标准方程.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
20.下列函数中,在区间($\frac{π}{2}$,π)上为增函数的是( )
| A. | y=sinx | B. | y=cosx | C. | y=tanx | D. | y=-tanx |
14.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x∈(-∞,0]}\\{{x}^{2}+2ax+1,x∈(0,+∞)}\end{array}\right.$,若函数g(x)=f(x)+2x-a有三个零点,则实数a的取值范围是( )
| A. | (0,+∞) | B. | (-∞,-1) | C. | (-∞,-3) | D. | (0,-3) |
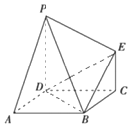 如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)
如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)