题目内容
7.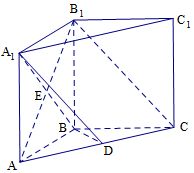 如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;
如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD;(Ⅰ)求证:BD⊥平面A1ACC1;
(Ⅱ)若AB=1,且AC•AD=1,求三棱锥A-BCB1的体积.
分析 (Ⅰ)连结ED,证明:BD⊥AC,A1A⊥BD,即可证明BD⊥平面A1ACC1;
(Ⅱ)若AB=1,且AC•AD=1,利用体积公式求三棱锥A-BCB1的体积.
解答 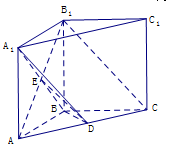 (Ⅰ)证明:连结ED(1分)
(Ⅰ)证明:连结ED(1分)
∵平面AB1C∩平面A1BD=ED,B1C∥平面A1BD,
∴B1C∥ED,---------------------------------------------(3分)
∵E为AB1中点,∴D为AC中点,
∵AB=BC,∴BD⊥AC①,-------------------------------(4分)
由A1A⊥平面ABC,BD?平面ABC,得A1A⊥BD②,
由①②及A1A、AC是平面A1ACC1内的两条相交直线,
得BD⊥平面A1ACC1.-------------------------------------------(6分)
(Ⅱ)解:由AB=1得BC=BB1=1,
由(Ⅰ)知$DA=\frac{1}{2}AC$,又AC•DA=1得AC2=2,----------------------------------------(8分)
∵AC2=2=AB2+BC2,∴AB⊥BC,---------------------------------------------------(10分)
∴${S_{△ABC}}=\frac{1}{2}AB•BC=\frac{1}{2}$
∴${V_{A-BC{B_1}}}=\frac{1}{3}{S_{△ABC}}•B{B_1}=\frac{1}{3}×\frac{1}{2}×1=\frac{1}{6}$.---------------------------------------------------------(12分)
点评 本题主要考查了线面平行性质和线面垂直的判定定理的应用,三棱锥体积的计算.考查了学生立体几何综合素质.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | (10,7) | B. | (10,5) | C. | (-4,-3) | D. | (-4,-1) |
| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
| A. | 55 | B. | 56 | C. | 57 | D. | 58 |
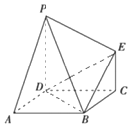 如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)
如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)