题目内容
6.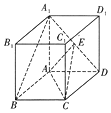 如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上,且E为A1D的中点
如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上,且E为A1D的中点(Ⅰ)求证:AA1⊥平面ABCD;
(Ⅱ)求三棱锥D-ACE的体积VD-ACE.
分析 (I)使用菱形的性质和勾股定理的逆定理证明AA1⊥AB,AA1⊥AD,从而得出AA1⊥平面ABCD;
(II)设AD的中点为F,连接EF,利用体积公式求三棱锥D-ACE的体积VD-ACE.
解答  (Ⅰ)证明:∵底面ABCD是菱形,∠ABC=60°,∴AB=AD=AC=2,
(Ⅰ)证明:∵底面ABCD是菱形,∠ABC=60°,∴AB=AD=AC=2,
∵AA1=2,∴AA12+AB2=A1B2,∴AA1⊥AB.
同理,AA1⊥AD,又∵AB?平面ABCD,AD?平面ABCD,AB∩AD=A,
∴AA1⊥平面ABCD.
(Ⅱ)解:设AD的中点为F,连接EF,则EF∥AA1,∴EF⊥平面ACD,且EF=1.
∴VD-ACE=VE-ACD=$\frac{1}{3}×1×\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面平行,线面垂直的判定,棱锥的体积计算,属于基础题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
16. 如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )
 如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
14.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x∈(-∞,0]}\\{{x}^{2}+2ax+1,x∈(0,+∞)}\end{array}\right.$,若函数g(x)=f(x)+2x-a有三个零点,则实数a的取值范围是( )
| A. | (0,+∞) | B. | (-∞,-1) | C. | (-∞,-3) | D. | (0,-3) |
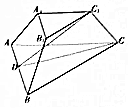 已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.
已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.