题目内容
7.解关于x的不等式 $\frac{ax}{x-1}<\frac{a-1}{x-1}$(a∈R)分析 讨论a=0与a>0和a<0时,对应不等式的解集是什么,分别求出即可.
解答 解:原不等式可化为(x-1)[ax-(a-1)]<0,
(1)当a=0时,原不等式为x-1<0,即x<1.
(2)当a≠0时,方程(x-1)[ax-(a-1)]=0的两根为x1=1,x2=$\frac{a-1}{a}$,所以1-$\frac{a-1}{a}$=$\frac{1}{a}$.
①当a>0时,$\frac{1}{a}$>0,所以1>$\frac{a-1}{a}$.
此时不等式的解集为{x|$\frac{a-1}{a}$<x<1};
②当a<0时,$\frac{1}{a}$<0,所以1<$\frac{a-1}{a}$.
此时原不等式化为(x-1)[-ax+(a-1)]>0,不等式的解集为{x|x>$\frac{a-1}{a}$,或x<1}.
综上所述,当a>0时,不等式的解集为{x|$\frac{a-1}{a}$<x<1};
当a=0时,不等式的解集为{x|x<1};
当a<0时,不等式的解集为{x|x>$\frac{a-1}{a}$,或x<1}.
点评 本题考查了含有字母系数的不等式的解法与应用问题,解题时应对字母系数进行讨论,是中档题目

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
19.已知命题p:3≥3;q:3>4,则下列选项正确的是( )
| A. | p或q为假,p且q为假,非p为真 | B. | p或q为真,p且q为假,非 p为真 | ||
| C. | p或q为假,p且q为假,非p为假 | D. | p或q为真,p且q为假,非p为假 |
16.用秦九韶算法求f(x)=3x5+8x4-3x3+5x2+12x-6,当x=2时,V3的值为( )
| A. | 55 | B. | 56 | C. | 57 | D. | 58 |
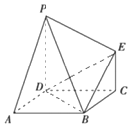 如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)
如图,四边形ABCD为正方形,PD⊥平面ABCD,CE⊥平面ABCD,CE=AB,PD=λCE(λ>1)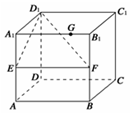 在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.
在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$. 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=60°,AB=2AD,PD⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=60°,AB=2AD,PD⊥底面ABCD.