题目内容
设复数z1=1+i,z2=2+bi,其中i为虚数单位,若z1•z2为实数,则实数b=( )
| A、-2 | B、-1 | C、1 | D、2 |
考点:复数的基本概念
专题:数系的扩充和复数
分析:由题意可得z1•z2=2-b+(2+b)i,由实数的定义可得2+b=0,解方程可得.
解答:
解:∵z1=1+i,z2=2+bi,
∴z1•z2=(1+i)(2+bi)=2-b+(2+b)i,
∵z1•z2为实数,∴2+b=0,解得b=-2
故选:A
∴z1•z2=(1+i)(2+bi)=2-b+(2+b)i,
∵z1•z2为实数,∴2+b=0,解得b=-2
故选:A
点评:本题考查复数的基本概念,属基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
下列结论正确的是( )
| A、命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4=0” |
| B、“x=4”是“x2-3x-4=0”的充分不必要条件 |
| C、已知命题p“若m>0,则方程x2+x-m=0有实根”,则命题p的否定¬p为真命题 |
| D、命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2=0,则m≠0或n≠0” |
b>0是函数f(x)=x2+bx+c在[0,+∞)单调的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f(x)=
的定义域为M,g(x)=
的定义域为N,则M∩N=( )
| 1 | ||
|
| x+2 |
| A、[-2,+∞) |
| B、[-2,2) |
| C、(-2,2) |
| D、(-∞,2) |
命题“对任意的x∈R,都有2x2-x+1≥0”的否定是( )
| A、对任意的x∈R,都有2x2-x+1<0 |
| B、存在x0∈R,使得2x02-x0+1<0 |
| C、不存在x0∈R,使得2x02-x0+1<0 |
| D、存在x0∈R,使得2x02-x0+1≥0 |
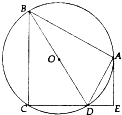 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.