题目内容
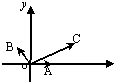如图所示，|| OA |
| OB |
| OA |
| OB |
| OC |
| OA |
| OC |
| OC |
| OA |
| OB |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：直接求λ+μ的值有难度，可换一角度，把
利用向量加法的平行四边形法则或三角形法则来表示成与
、
，共线的其它向量的和向量，再由平面向量基本定理，进而求出λ+μ的值
| OC |
| OA |
| OB |
解答：
解：如图所示，A（1，0），由∠COA=300，所以C(5cos300，5sin300)，即C(
，
)，B(-
，
)，
=m
+n
，即(
，
)=m(1，0)+n(-
，
)
，
．∴
=
+
，∴m=
，n=
．
5
| ||
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| OC |
| OA |
| OB |
5
| ||
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
|
|
| OC |
10
| ||
| 3 |
| OA |
5
| ||
| 3 |
| OB |
10
| ||
| 3 |
5
| ||
| 3 |
点评：本题考查平面向量加法的平行四边形法则与三角形法则，及解三角形，是一道综合题，是本部分的重点也是难点．夯实基础是关键
练习册系列答案
相关题目
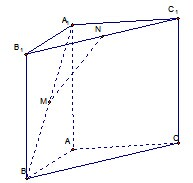如图，直三棱柱ABC-A1B1C1，∠BAC=90°，AB=AC=
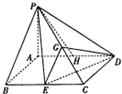已知在四棱锥P-ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，PA=