题目内容
(坐标系与参数方程选做题)在极坐标系(ρ,θ)(0≤θ≤2π)中,点P(2,
) 到直线ρcos(θ-
)=
的距离等于 .
| 5π |
| 4 |
| π |
| 4 |
| 2 |
考点:简单曲线的极坐标方程,点到直线的距离公式,点的极坐标和直角坐标的互化
专题:计算题
分析:化点、直线的极坐标为直角坐标,利用点到直线的距离公式,我们可以得到结论.
解答:
解:点P(2,
)的直角坐标为(-
,-
)
直线ρcos(θ-
)=
的直角坐标方程为:x+y-2=0
利用点到直线的距离公式可得:d=
=2+
.
故答案为:2+
.
| 5π |
| 4 |
| 2 |
| 2 |
直线ρcos(θ-
| π |
| 4 |
| 2 |
利用点到直线的距离公式可得:d=
|-
| ||||
|
| 2 |
故答案为:2+
| 2 |
点评:极坐标中的问题,通常是转化为直角坐标,进行解决,掌握转化公式是解决这类问题的关键.

练习册系列答案
相关题目
二次函数y=a(a+1)x2-(2a+1)x+1,当a=1,2,3,…,n,…时,其图象在x轴上截得的弦长依次为d1,d2,…,dn,…,则d1+d2+…+dn为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若实数x,y满足不等式
,则z=2x+y的最大值为( )
|
| A、1 | B、3 | C、4 | D、5 |
已知某个几何体的三视图如右,那么可得这个几何体的体积是( )
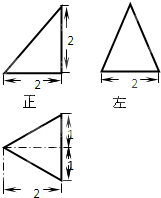

A、
| ||
B、
| ||
C、
| ||
D、
|