题目内容
已知在三棱柱ABC-A1B1C1中，
=4
，
=
，
=
，面BCE、面ACF、面ABG相交于点O，则三棱柱的体积：三棱锥O-ABC= ．
| AE |
| EA1 |
| BF |
| FB1 |
| CG |
| GC1 |
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：如图所示，由已知可得：平面BCE与平面ACF的交线是CM，平面ABG与平面ACF的交线是AN．则CM与AN的交点即为O点．由于
=4
，
=
，
=
，可得点N是CF的中点，
=
=
．过点N作NP∥AF交CM于点P．可得
=
．分别设点O，N，C1到底面的距离为hO，hN，hC1．可得hO：hN：hC1=3：4：16．即可得出三棱柱的体积：三棱锥O-ABC=
．
| AE |
| EA1 |
| BF |
| FB1 |
| CG |
| GC1 |
| FM |
| AM |
| BF |
| AE |
| 2 |
| 3 |
| AO |
| AN |
| 3 |
| 4 |
| S△ABC•hC1 | ||
|
解答：
解：如图所示，
由已知可得：平面BCE与平面ACF的交线是CM，
平面ABG与平面ACF的交线是AN．
则CM与AN的交点即为O点．
∵
=4
，
=
，
=
，
∴点N是CF的中点，
=
=
．
过点N作NP∥AF交CM于点P．
则
=
=
，
=
，
∴
=
．
∴
=
．
分别设点O，N，C1到底面的距离为hO，hN，hC1．
则hO：hN：hC1=3：4：16．
∴三棱柱的体积：三棱锥O-ABC=
=
．
故答案为：16．
由已知可得：平面BCE与平面ACF的交线是CM，
平面ABG与平面ACF的交线是AN．
则CM与AN的交点即为O点．
∵
| AE |
| EA1 |
| BF |
| FB1 |
| CG |
| GC1 |
∴点N是CF的中点，
| FM |
| AM |
| BF |
| AE |
| 2 |
| 3 |
过点N作NP∥AF交CM于点P．
则
| NP |
| MF |
| CN |
| CF |
| 1 |
| 2 |
| ON |
| OA |
| NP |
| AM |
∴
| ON |
| OA |
| 1 |
| 3 |
∴
| AO |
| AN |
| 3 |
| 4 |
分别设点O，N，C1到底面的距离为hO，hN，hC1．
则hO：hN：hC1=3：4：16．
∴三棱柱的体积：三棱锥O-ABC=
| S△ABC•hC1 | ||
|
| 16 |
| 1 |
故答案为：16．
点评：本题考查了平面的交线、平行线分线段成比例定理、面积比与对应边的比、三棱柱与三棱锥的体积计算公式，考查了作图能力与推理能力、计算能力，考查了空间想象能力，属于难题．
练习册系列答案
单元期中期末卷系列答案
相关题目
函数y=ax+1（a＞0且a≠1）的图象必经过点（ ）
| A、（0，1） |
| B、（1，0） |
| C、（2，1） |
| D、（0，2） |
具有性质：f（
）=-f（x）的函数，我们称为满足“倒负”交换的函数，则下列函数：①y=x-
；②y=x+
；③y=lnx；④y=
中所有满足“到负”交换的函数是（ ）
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
|
| A、①③ | B、②④ | C、①④ | D、①③④ |
已知两异面直线a，b的夹角是15°，过空间一点P作直线l，使得l与a，b的夹角均为8°，那么这样的直线l有（ ）
| A、3条 | B、2条 | C、1条 | D、0条 |
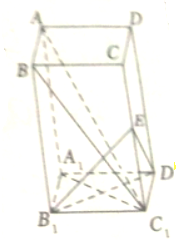在长方体ABCD-A1B1C1D1中，E∈CC1，B1E⊥BC1，AB=CD，求证：AC1⊥面B1ED1．
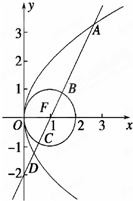已知抛物线M：y2=4x，圆F：（x-1）2+y2=1，过点F作直线l，自上而下依次与上述两曲线交于点A，B，C，D（如图所示），T（-1，0）．