题目内容
函数y=f(x)的图象连续且在区间[a,b]上的左右端点分别为A和B,点M(x0,y0)是该图象上的一点,且x0=λa+(1-λ)b,λ∈[0,1],令向量
=λ
+(1-λ)
,若|
|有最大值k,则称函数f(x)在[a,b]上“k阶线性近似”.若函数f(x)=x2+1在区间[0,1]上“k阶线性近似”,则实数k= .
| ON |
| OA |
| OB |
| MN |
考点:利用导数研究函数的单调性
专题:转化思想,函数的性质及应用
分析:由题意可得,若A、B是f(x)=x2+1图象上横坐标分别为a、b的两点,则A(0,1),B(1,2),由两点式求出AB的方程,代入|
|=|x2+1-x-1|求其最大值得答案.
| MN |
解答:
解:由题意,M、N横坐标相等,|
|有最大值k,则为|
|的最大值,
函数f(x)=x2+1在区间[0,1]上“k阶线性近似”,
由A、B是其图象上横坐标分别为a、b的两点,则A(0,1),B(1,2),
∴直线AB方程为y=x+1
∴|
|=|x2+1-x-1|=|x2-x|∈[0,
].
∴实数k=
.
故答案为:
.
| MN |
| MN |
函数f(x)=x2+1在区间[0,1]上“k阶线性近似”,
由A、B是其图象上横坐标分别为a、b的两点,则A(0,1),B(1,2),
∴直线AB方程为y=x+1
∴|
| MN |
| 1 |
| 4 |
∴实数k=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:题考查向量知识的运用,考查函数最值求解,解答的关键理解新概念,将已知条件进行转化,是难题.

练习册系列答案
相关题目
下列函数与y=
是同一函数的是( )
| 1 |
| x |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=aloga
|
椭圆
+
=1(a>b>0)上一点A关于原点的对称点为B,!F为其左焦点,若AF⊥BF,设∠ABF=
,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|
在空间中,a,b是不重合的直线,α,β是不重合的平面,则下列条件中可推出a∥b的是( )
| A、a?α,b?β,α∥β |
| B、a∥α,b?β |
| C、a⊥α,b⊥β |
| D、a⊥α,b?α |
 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠BAC=90°,AB=AC=AA1=6,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠BAC=90°,AB=AC=AA1=6,D为BC的中点.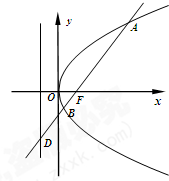 如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.
如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.