题目内容
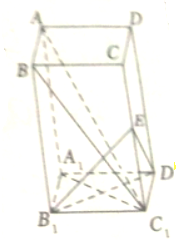在长方体ABCD-A1B1C1D1中，E∈CC1，B1E⊥BC1，AB=CD，求证：AC1⊥面B1ED1．考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：连接A1C1，证明AC1⊥B1D1．AC1⊥B1E，利用直线与平面垂直的判定定理证明AC1⊥平面EB1D1；
解答：
证明：连接A1C1，由条件得A1B1C1D1是正方形，因此B1D1⊥A1C1，
又AA1⊥平面A1B1C1D1，所以AA1⊥B1D1，因此B1D1⊥平面AA1C1，
所以AC1⊥B1D1．同理可证：AC1⊥B1E．B1D1∩B1E=B1，
所以AC1⊥平面EB1D1．
又AA1⊥平面A1B1C1D1，所以AA1⊥B1D1，因此B1D1⊥平面AA1C1，
所以AC1⊥B1D1．同理可证：AC1⊥B1E．B1D1∩B1E=B1，
所以AC1⊥平面EB1D1．
点评：本题考查直线与平面垂直的判定定理的应用，考查空间想象能力以及计算能力．
练习册系列答案
小学教材完全解读系列答案
相关题目
已知三棱柱ABC-A1B1C1，侧棱AA1垂直于底面ABC，∠BAC=90°，AB=AC=AA1=6，D为BC的中点．在空间中，a，b是不重合的直线，α，β是不重合的平面，则下列条件中可推出a∥b的是（ ）
| A、a?α，b?β，α∥β |
| B、a∥α，b?β |
| C、a⊥α，b⊥β |
| D、a⊥α，b?α |
函数f（x）=
+
的定义域为（ ）
| 1-2x |
| 1 | ||
|
| A、（-3，0] |
| B、（-3，1] |
| C、（-∞，-3）∪（-3，0] |
| D、（-∞，-3）∪（-3，1] |