Question

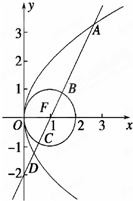已知抛物线M：y²=4x，圆F：（x-1）²+y²=1，过点F作直线l，自上而下依次与上述两曲线交于点A，B，C，D（如图所示），T（-1，0）．
（Ⅰ）求|AB|•|CD|；
（Ⅱ）作D关于x轴的对称点M，求证：T，A，M三点共线；
（Ⅲ）作C关于x轴的对称点S，求S到直线l的距离的最大值．

Answer 1

考点：抛物线的应用

专题：计算题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）由题意设直线l：x=ty+1，设A（x₁，y₁），D（x₂，y₂），从而表示出|AB|•|CD|，化简即可；
（Ⅱ）由题意点M（x₂，-y₂），表示出向量

TA

，

TM

，从而证明T，A，M三点共线；
（Ⅲ）由题意求出点C，从而表示出点S，写出S到直线l的距离，利用基本不等式求最大值．

解答： 解：（Ⅰ）设直线l：x=ty+1，
代入抛物线方程得，y²-4ty-4=0，
设A（x₁，y₁），D（x₂，y₂），
则|AF|=x₁+1，|DF|=x₂+1；
故|AB|=x₁，|CD|=x₂；
∴|AB|•|CD|=x₁x₂=

(y1y2)2

16

；
而y₁y₂=-4，代入上式可得，
|AB|•|CD|=

(y1y2)2

16

=1；
（Ⅱ）证明：由题意，点M（x₂，-y₂），

TA

=（1+x₁，y₁），

TM

=（1+x₂，-y₂），
又∵y₁y₂=-4，y₁+y₂=4t，
∴（1+x₁）（-y₂）-（1+x₂）y₁
=（2+ty₁）（-y₂）-（ty₂+2）y₁
=2ty₁y₂-2（y₁+y₂）=0．
故T，A，M三点共线；
（Ⅲ）将直线l：x=ty+1，代入圆的方程，
（1+t²）y²=1，
y_C=

-1

1+t2

，x_C=1-

t

1+t2

；
点S（1-

t

1+t2

，-

-1

1+t2

）到直线l的距离d=

|2t|

1+t2

，
当t≠0时，
d=

2

1 |t| +|t|

≤

2

2

=1，（当且仅当|t|=1时，等号成立）
故S到直线l的距离的最大值为1．

点评：本题考查了圆锥曲线的性质应用，同时考查了函数的最值，属于难题．