题目内容
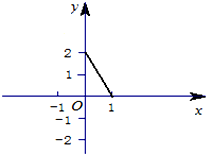 已知函数y=f(x)是定义在[-1,1]上的奇函数,当x∈(0,1]时的图象如图所示.
已知函数y=f(x)是定义在[-1,1]上的奇函数,当x∈(0,1]时的图象如图所示.(1)画出函数在[-1,0)上的图象;
(2)求函数y=f(x)的解析式.
考点:函数解析式的求解及常用方法,函数的图象
专题:计算题,函数的性质及应用
分析:(1)由奇函数的图象关于原点对称可作出函数在[-1,0)上的图象;
(2)只需求出∈[-1,0]上的解析式即可.当x∈[-1,0)时由奇函数的性质可求;当x=0时由f(-0)=-f(0)可求;
(2)只需求出∈[-1,0]上的解析式即可.当x∈[-1,0)时由奇函数的性质可求;当x=0时由f(-0)=-f(0)可求;
解答:
 解:(1)函数在[-1,0)上的图象如图所示:
解:(1)函数在[-1,0)上的图象如图所示:
(2)依题意知:当x∈(0,1]时,
函数图象所在直线过点(1,0),(0,2),其方程为y=-2x+2,
∴当x∈(0,1]时,函数的解析式为f(x)=-2x+2,
当x∈[-1,0)时,-x∈(0,1],
故有f(-x)=-2(-x)+2=2x+2,即当x∈[-1,0)时,f(x)=-2x-2,
当x=0时,由f(-0)=-f(0),得f(0)=0.
∴f(x)=
.
 解:(1)函数在[-1,0)上的图象如图所示:
解:(1)函数在[-1,0)上的图象如图所示:(2)依题意知:当x∈(0,1]时,
函数图象所在直线过点(1,0),(0,2),其方程为y=-2x+2,
∴当x∈(0,1]时,函数的解析式为f(x)=-2x+2,
当x∈[-1,0)时,-x∈(0,1],
故有f(-x)=-2(-x)+2=2x+2,即当x∈[-1,0)时,f(x)=-2x-2,
当x=0时,由f(-0)=-f(0),得f(0)=0.
∴f(x)=
|
点评:该题考查函数的奇偶性及其应用,考查函数解析式的求解,考查数形结合思想,属基础题.

练习册系列答案
相关题目
 某农场有如图所示的六块田地,现有萝卜、玉米、油菜三类蔬菜可种.为有利于作物生长,要求每块田地种一类蔬菜,每类蔬菜种两块田地,每行、每列的蔬菜种类各不相同.则不同的种植方法数为( )
某农场有如图所示的六块田地,现有萝卜、玉米、油菜三类蔬菜可种.为有利于作物生长,要求每块田地种一类蔬菜,每类蔬菜种两块田地,每行、每列的蔬菜种类各不相同.则不同的种植方法数为( ) 如图,在直平行六面体ABCD-A1B1C1D1中,侧棱AA1=3,AB=3,BC=
如图,在直平行六面体ABCD-A1B1C1D1中,侧棱AA1=3,AB=3,BC=