题目内容
某农场有如图所示的六块田地，现有萝卜、玉米、油菜三类蔬菜可种．为有利于作物生长，要求每块田地种一类蔬菜，每类蔬菜种两块田地，每行、每列的蔬菜种类各不相同．则不同的种植方法数为（ ）| A、12 | B、16 | C、18 | D、24 |
考点：计数原理的应用
专题：排列组合
分析：第一步先种第一行，第二步再种第二行，第一列只能从剩下的两种蔬菜选择一种，第一列确定后，第二行也就确定了，根据分步计数原理可得
解答：
解：第一步先种第一行有
=6种，
第二步再种第二行，第一列只能从剩下的两种蔬菜选择一种，第一列确定后，第二行也就确定了，有2种，
根据分步计数原理可得6×2=12种．
故选：A．
| A | 3 3 |
第二步再种第二行，第一列只能从剩下的两种蔬菜选择一种，第一列确定后，第二行也就确定了，有2种，
根据分步计数原理可得6×2=12种．
故选：A．
点评：本题主要考查了分步计数原理，关键是确第二行的第一快地，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
则方程f（x）=ax恰有两个不同的实根时，实数a的取值范围是（注：e为自然对数的底数）（ ）
|
| A、（-1，0） | ||||
B、（-1，
| ||||
C、（-1，0）∪（
| ||||
D、（-1，
|
圆O的弦AB，CD相交于点P，已知P是AB的中点，AB=12，PC=4，那么PD=（ ）
| A、16 | B、9 | C、8 | D、4 |
要得到函数y=2sin2x的图象，只需将函数y=2sin（2x-
）的图象（ ）
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
若P的Q的北偏东44°50′，则Q在P的（ ）
| A、东偏北45°10′ |
| B、东偏北45°50′ |
| C、南偏西44°50′ |
| D、西偏南45°50′ |
如图，直三棱柱ABC-A1B1C1底面边长均为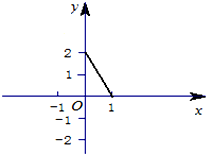
已知函数y=f（x）是定义在[-1，1]上的奇函数，当x∈（0，1]时的图象如图所示．