题目内容
以直线x-y=0与x-3y+2=0的交点A,及B(0,4),C(3,0)组成三角形ABC,AD为BC边上的高,垂足为D,求AD所在直线方程及三角形ABC的面积.
考点:直线的一般式方程与直线的性质
专题:直线与圆
分析:求两条直线的交点A的坐标,根据两条直线垂直的性质求得AD的斜率,用点斜式求得AD的方程.用截距式求得BC的方程,再利用点到直线的距离公式求出A到直线BC的距离d,从而求得S△ABC=
BC•d 的值.
| 1 |
| 2 |
解答:
解:由
求得A(1,1),由于BC所在直线的斜率为
-
,
所以高线AD直线斜率为
,所以AD直线所在方程为y-1=
(x-1),即 3x-4y+1=0.
直线BC的方程为
+
=1,即4x+3y-12=0,点A到BC直线的距离d=
=1,BC=5,
∴S△ABC=
BC•d=
=
.
|
| 4-0 |
| 0-3 |
| 4 |
| 3 |
所以高线AD直线斜率为
| 3 |
| 4 |
| 3 |
| 4 |
直线BC的方程为
| x |
| 3 |
| y |
| 4 |
| |4+3-12| | ||
|
∴S△ABC=
| 1 |
| 2 |
| 1×5 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查求两条直线的交点,两条直线垂直的性质,点到直线的距离公式,属于基础题.

练习册系列答案
相关题目
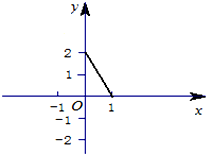 已知函数y=f(x)是定义在[-1,1]上的奇函数,当x∈(0,1]时的图象如图所示.
已知函数y=f(x)是定义在[-1,1]上的奇函数,当x∈(0,1]时的图象如图所示.